Improving embedding of graphs with missing data by soft manifolds

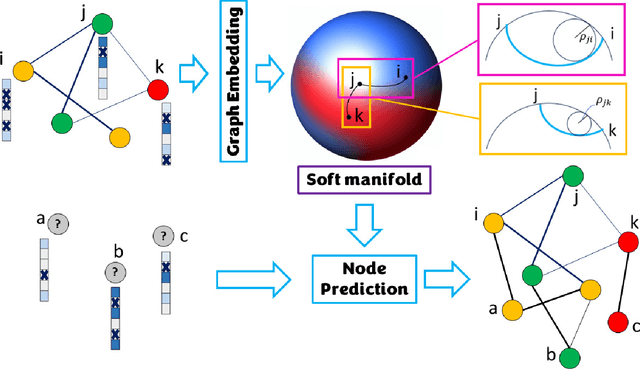
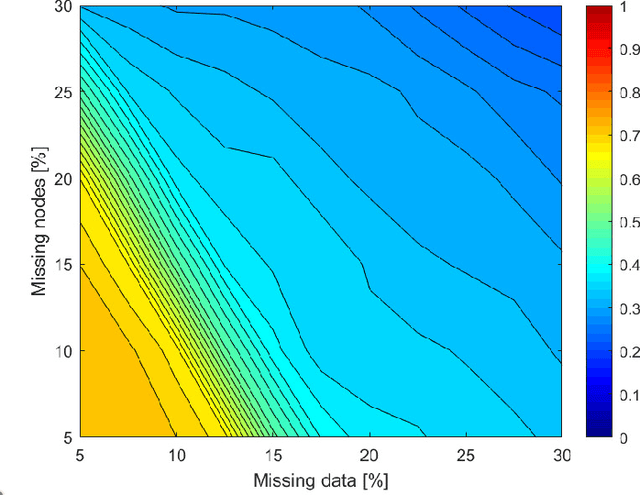
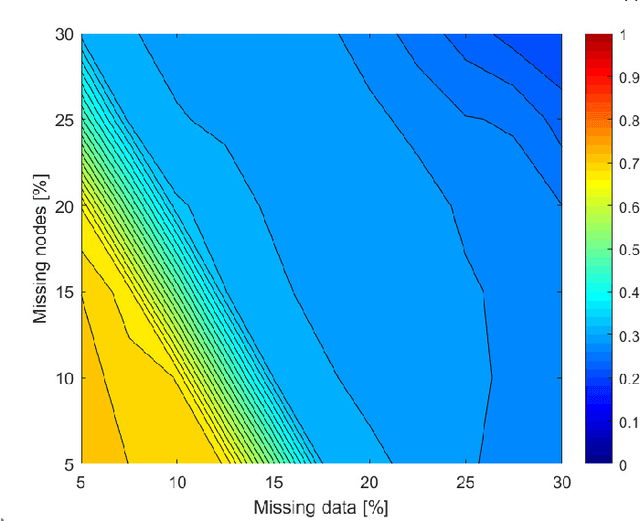
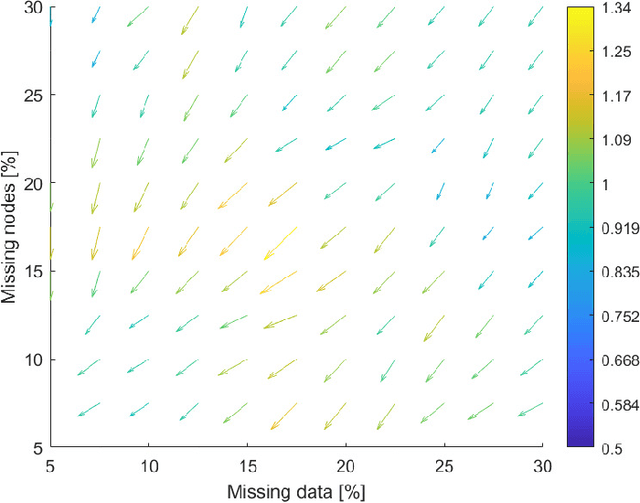
Embedding graphs in continous spaces is a key factor in designing and developing algorithms for automatic information extraction to be applied in diverse tasks (e.g., learning, inferring, predicting). The reliability of graph embeddings directly depends on how much the geometry of the continuous space matches the graph structure. Manifolds are mathematical structure that can enable to incorporate in their topological spaces the graph characteristics, and in particular nodes distances. State-of-the-art of manifold-based graph embedding algorithms take advantage of the assumption that the projection on a tangential space of each point in the manifold (corresponding to a node in the graph) would locally resemble a Euclidean space. Although this condition helps in achieving efficient analytical solutions to the embedding problem, it does not represent an adequate set-up to work with modern real life graphs, that are characterized by weighted connections across nodes often computed over sparse datasets with missing records. In this work, we introduce a new class of manifold, named soft manifold, that can solve this situation. In particular, soft manifolds are mathematical structures with spherical symmetry where the tangent spaces to each point are hypocycloids whose shape is defined according to the velocity of information propagation across the data points. Using soft manifolds for graph embedding, we can provide continuous spaces to pursue any task in data analysis over complex datasets. Experimental results on reconstruction tasks on synthetic and real datasets show how the proposed approach enable more accurate and reliable characterization of graphs in continuous spaces with respect to the state-of-the-art.

Electrode Selection for Noninvasive Fetal Electrocardiogram Extraction using Mutual Information Criteria

Blind source separation (BSS) techniques have revealed to be promising approaches for, among other, biomedical signal processing applications. Specifically, for the noninvasive extraction of fetal cardiac signals from maternal abdominal recordings, where conventional filtering schemes have failed to extract the complete fetal ECG components. From previous studies, it is now believed that a carefully selected array of electrodes well-placed over the abdomen of a pregnant woman contains the required `information' for BSS, to extract the complete fetal components. Based on this idea, in previous works array recording systems and sensor selection strategies based on the Mutual Information (MI) criterion have been developed. In this paper the previous works have been extended, by considering the 3-dimensional aspects of the cardiac electrical activity. The proposed method has been tested on simulated and real maternal abdominal recordings. The results show that the new sensor selection strategy together with the MI criterion, can be effectively used to select the channels containing the most `information' concerning the fetal ECG components from an array of 72 recordings. The method is hence believed to be useful for the selection of the most informative channels in online applications, considering the different fetal positions and movements.

A graph representation based on fluid diffusion model for multimodal data analysis: theoretical aspects and enhanced community detection

Representing data by means of graph structures identifies one of the most valid approach to extract information in several data analysis applications. This is especially true when multimodal datasets are investigated, as records collected by means of diverse sensing strategies are taken into account and explored. Nevertheless, classic graph signal processing is based on a model for information propagation that is configured according to heat diffusion mechanism. This system provides several constraints and assumptions on the data properties that might be not valid for multimodal data analysis, especially when large scale datasets collected from heterogeneous sources are considered, so that the accuracy and robustness of the outcomes might be severely jeopardized. In this paper, we introduce a novel model for graph definition based on fluid diffusion. The proposed approach improves the ability of graph-based data analysis to take into account several issues of modern data analysis in operational scenarios, so to provide a platform for precise, versatile, and efficient understanding of the phenomena underlying the records under exam, and to fully exploit the potential provided by the diversity of the records in obtaining a thorough characterization of the data and their significance. In this work, we focus our attention to using this fluid diffusion model to drive a community detection scheme, i.e., to divide multimodal datasets into many groups according to similarity among nodes in an unsupervised fashion. Experimental results achieved by testing real multimodal datasets in diverse application scenarios show that our method is able to strongly outperform state-of-the-art schemes for community detection in multimodal data analysis.

Temporally Nonstationary Component Analysis; Application to Noninvasive Fetal Electrocardiogram Extraction

Objective: Mixtures of temporally nonstationary signals are very common in biomedical applications. The nonstationarity of the source signals can be used as a discriminative property for signal separation. Herein, a semi-blind source separation algorithm is proposed for the extraction of temporally nonstationary components from linear multichannel mixtures of signals and noises. Methods: A hypothesis test is proposed for the detection and fusion of temporally nonstationary events, by using ad hoc indexes for monitoring the first and second order statistics of the innovation process. As proof of concept, the general framework is customized and tested over noninvasive fetal cardiac recordings acquired from the maternal abdomen, over publicly available datasets, using two types of nonstationarity detectors: 1) a local power variations detector, and 2) a model-deviations detector using the innovation process properties of an extended Kalman filter. Results: The performance of the proposed method is assessed in presence of white and colored noise, in different signal-to-noise ratios. Conclusion and Significance: The proposed scheme is general and it can be used for the extraction of nonstationary events and sample deviations from a presumed model in multivariate data, which is a recurrent problem in many machine learning applications.

A Hypothesis Testing Approach to Nonstationary Source Separation

The extraction of nonstationary signals from blind and semi-blind multivariate observations is a recurrent problem. Numerous algorithms have been developed for this problem, which are based on the exact or approximate joint diagonalization of second or higher order cumulant matrices/tensors of multichannel data. While a great body of research has been dedicated to joint diagonalization algorithms, the selection of the diagonalized matrix/tensor set remains highly problem-specific. Herein, various methods for nonstationarity identification are reviewed and a new general framework based on hypothesis testing is proposed, which results in a classification/clustering perspective to semi-blind source separation of nonstationary components. The proposed method is applied to noninvasive fetal ECG extraction, as case study.

Enhancing ensemble learning and transfer learning in multimodal data analysis by adaptive dimensionality reduction

Modern data analytics take advantage of ensemble learning and transfer learning approaches to tackle some of the most relevant issues in data analysis, such as lack of labeled data to use to train the analysis models, sparsity of the information, and unbalanced distributions of the records. Nonetheless, when applied to multimodal datasets (i.e., datasets acquired by means of multiple sensing techniques or strategies), the state-of-theart methods for ensemble learning and transfer learning might show some limitations. In fact, in multimodal data analysis, not all observations would show the same level of reliability or information quality, nor an homogeneous distribution of errors and uncertainties. This condition might undermine the classic assumptions ensemble learning and transfer learning methods rely on. In this work, we propose an adaptive approach for dimensionality reduction to overcome this issue. By means of a graph theory-based approach, the most relevant features across variable size subsets of the considered datasets are identified. This information is then used to set-up ensemble learning and transfer learning architectures. We test our approach on multimodal datasets acquired in diverse research fields (remote sensing, brain-computer interfaces, photovoltaic energy). Experimental results show the validity and the robustness of our approach, able to outperform state-of-the-art techniques.

Dynamical spectral unmixing of multitemporal hyperspectral images

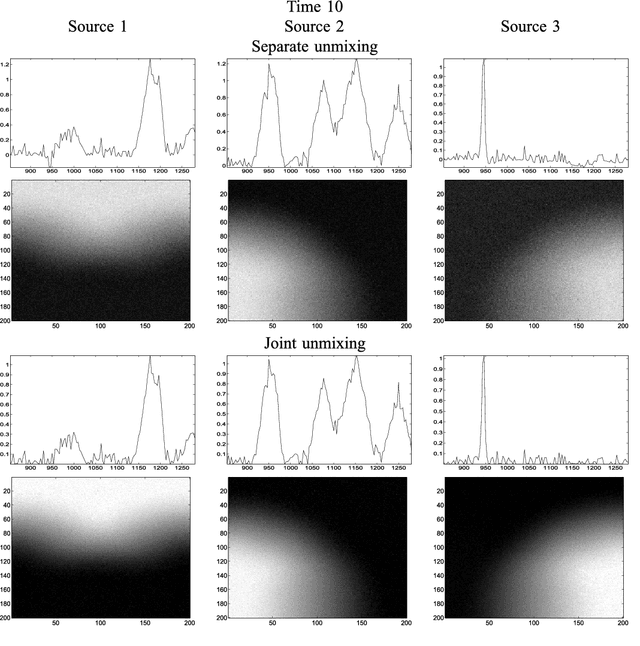
In this paper, we consider the problem of unmixing a time series of hyperspectral images. We propose a dynamical model based on linear mixing processes at each time instant. The spectral signatures and fractional abundances of the pure materials in the scene are seen as latent variables, and assumed to follow a general dynamical structure. Based on a simplified version of this model, we derive an efficient spectral unmixing algorithm to estimate the latent variables by performing alternating minimizations. The performance of the proposed approach is demonstrated on synthetic and real multitemporal hyperspectral images.

On the Achievability of Cramér-Rao Bound In Noisy Compressed Sensing

Recently, it has been proved in Babadi et al. that in noisy compressed sensing, a joint typical estimator can asymptotically achieve the Cramer-Rao lower bound of the problem.To prove this result, this paper used a lemma,which is provided in Akcakaya et al,that comprises the main building block of the proof. This lemma is based on the assumption of Gaussianity of the measurement matrix and its randomness in the domain of noise. In this correspondence, we generalize the results obtained in Babadi et al by dropping the Gaussianity assumption on the measurement matrix. In fact, by considering the measurement matrix as a deterministic matrix in our analysis, we find a theorem similar to the main theorem of Babadi et al for a family of randomly generated (but deterministic in the noise domain) measurement matrices that satisfy a generalized condition known as The Concentration of Measures Inequality. By this, we finally show that under our generalized assumptions, the Cramer-Rao bound of the estimation is achievable by using the typical estimator introduced in Babadi et al.

Fast Sparse Decomposition by Iterative Detection-Estimation

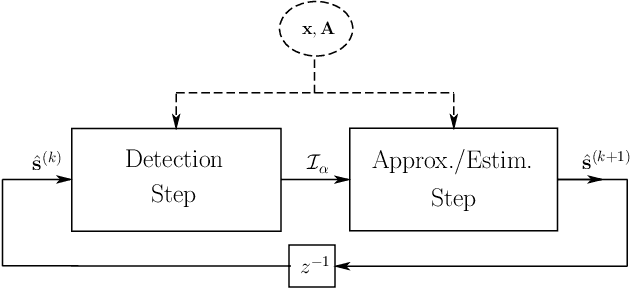
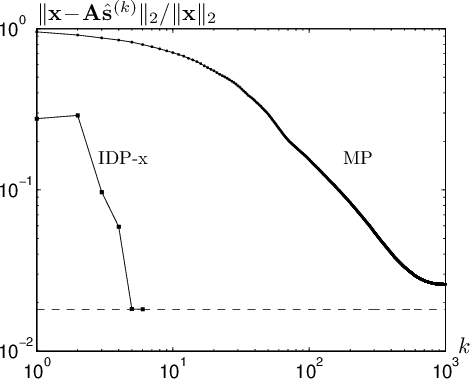
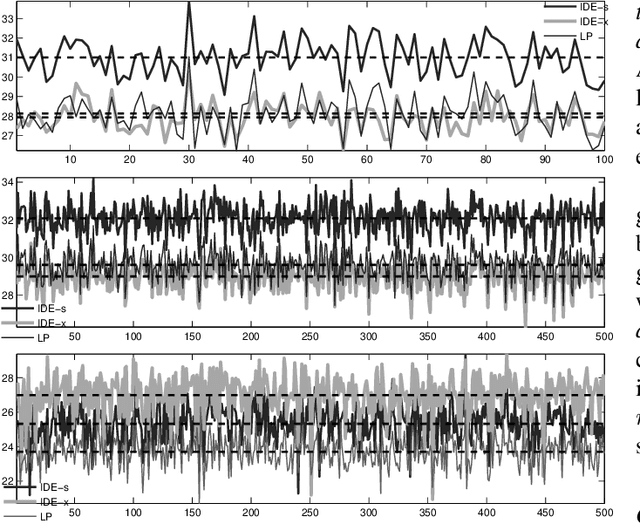
Finding sparse solutions of underdetermined systems of linear equations is a fundamental problem in signal processing and statistics which has become a subject of interest in recent years. In general, these systems have infinitely many solutions. However, it may be shown that sufficiently sparse solutions may be identified uniquely. In other words, the corresponding linear transformation will be invertible if we restrict its domain to sufficiently sparse vectors. This property may be used, for example, to solve the underdetermined Blind Source Separation (BSS) problem, or to find sparse representation of a signal in an `overcomplete' dictionary of primitive elements (i.e., the so-called atomic decomposition). The main drawback of current methods of finding sparse solutions is their computational complexity. In this paper, we will show that by detecting `active' components of the (potential) solution, i.e., those components having a considerable value, a framework for fast solution of the problem may be devised. The idea leads to a family of algorithms, called `Iterative Detection-Estimation (IDE)', which converge to the solution by successive detection and estimation of its active part. Comparing the performance of IDE(s) with one of the most successful method to date, which is based on Linear Programming (LP), an improvement in speed of about two to three orders of magnitude is observed.

A New Trend in Optimization on Multi Overcomplete Dictionary toward Inpainting

Recently, great attention was intended toward overcomplete dictionaries and the sparse representations they can provide. In a wide variety of signal processing problems, sparsity serves a crucial property leading to high performance. Inpainting, the process of reconstructing lost or deteriorated parts of images or videos, is an interesting application which can be handled by suitably decomposition of an image through combination of overcomplete dictionaries. This paper addresses a novel technique of such a decomposition and investigate that through inpainting of images. Simulations are presented to demonstrate the validation of our approach.