Dynamical spectral unmixing of multitemporal hyperspectral images
Paper and Code
Oct 14, 2015

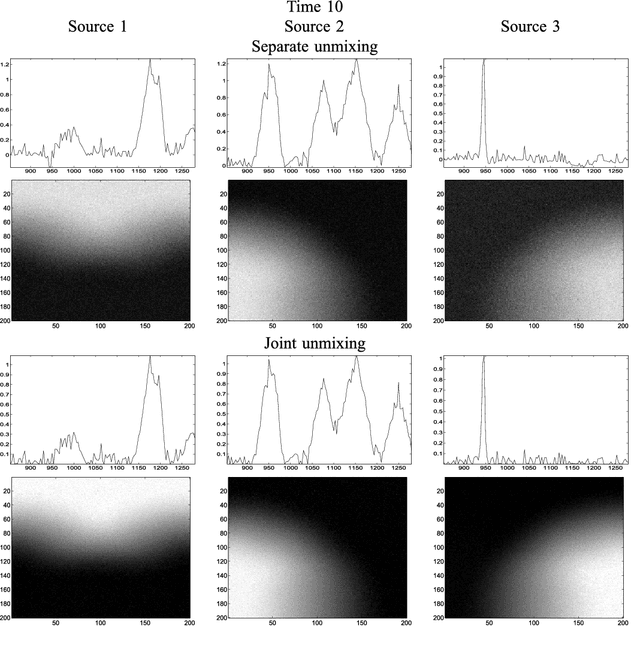

In this paper, we consider the problem of unmixing a time series of hyperspectral images. We propose a dynamical model based on linear mixing processes at each time instant. The spectral signatures and fractional abundances of the pure materials in the scene are seen as latent variables, and assumed to follow a general dynamical structure. Based on a simplified version of this model, we derive an efficient spectral unmixing algorithm to estimate the latent variables by performing alternating minimizations. The performance of the proposed approach is demonstrated on synthetic and real multitemporal hyperspectral images.
* 13 pages, 10 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge