Fast Sparse Decomposition by Iterative Detection-Estimation
Paper and Code
Sep 20, 2010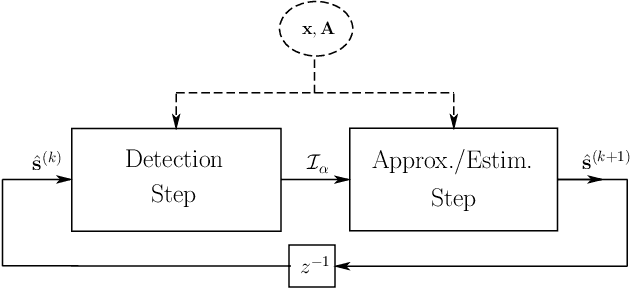

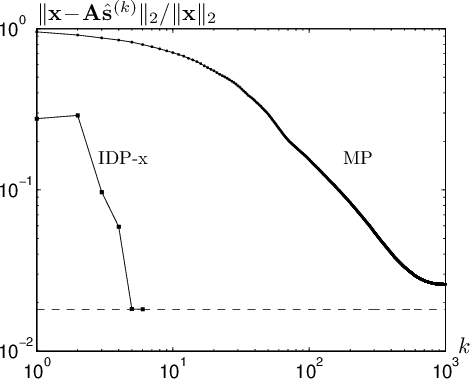
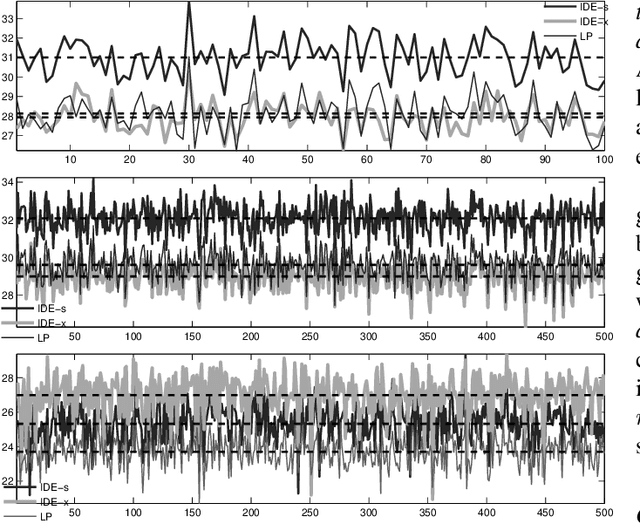
Finding sparse solutions of underdetermined systems of linear equations is a fundamental problem in signal processing and statistics which has become a subject of interest in recent years. In general, these systems have infinitely many solutions. However, it may be shown that sufficiently sparse solutions may be identified uniquely. In other words, the corresponding linear transformation will be invertible if we restrict its domain to sufficiently sparse vectors. This property may be used, for example, to solve the underdetermined Blind Source Separation (BSS) problem, or to find sparse representation of a signal in an `overcomplete' dictionary of primitive elements (i.e., the so-called atomic decomposition). The main drawback of current methods of finding sparse solutions is their computational complexity. In this paper, we will show that by detecting `active' components of the (potential) solution, i.e., those components having a considerable value, a framework for fast solution of the problem may be devised. The idea leads to a family of algorithms, called `Iterative Detection-Estimation (IDE)', which converge to the solution by successive detection and estimation of its active part. Comparing the performance of IDE(s) with one of the most successful method to date, which is based on Linear Programming (LP), an improvement in speed of about two to three orders of magnitude is observed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge