Massoud Babaie-Zadeh
Performance Guarantees for Schatten-$p$ Quasi-Norm Minimization in Recovery of Low-Rank Matrices
Oct 26, 2014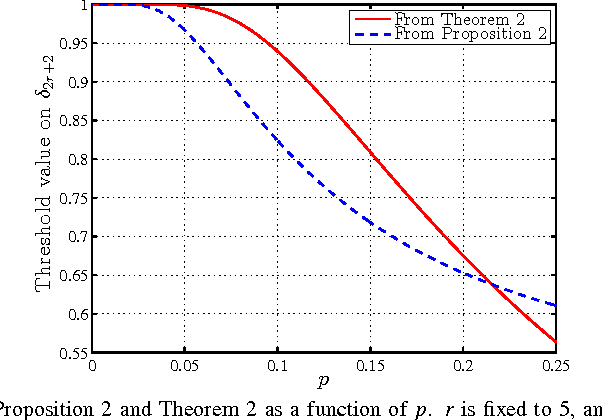
Abstract:We address some theoretical guarantees for Schatten-$p$ quasi-norm minimization ($p \in (0,1]$) in recovering low-rank matrices from compressed linear measurements. Firstly, using null space properties of the measurement operator, we provide a sufficient condition for exact recovery of low-rank matrices. This condition guarantees unique recovery of matrices of ranks equal or larger than what is guaranteed by nuclear norm minimization. Secondly, this sufficient condition leads to a theorem proving that all restricted isometry property (RIP) based sufficient conditions for $\ell_p$ quasi-norm minimization generalize to Schatten-$p$ quasi-norm minimization. Based on this theorem, we provide a few RIP-based recovery conditions.
Fast Sparse Decomposition by Iterative Detection-Estimation
Sep 20, 2010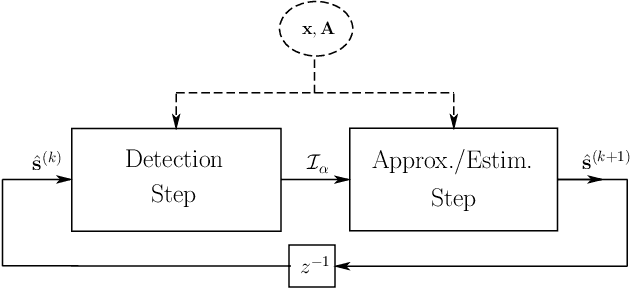

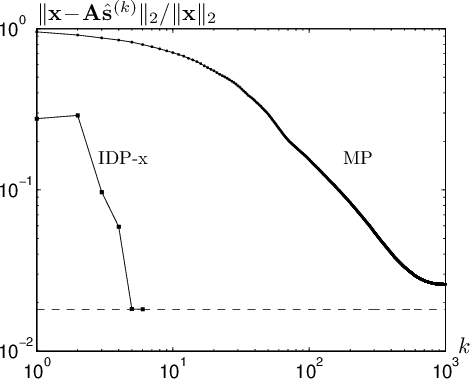
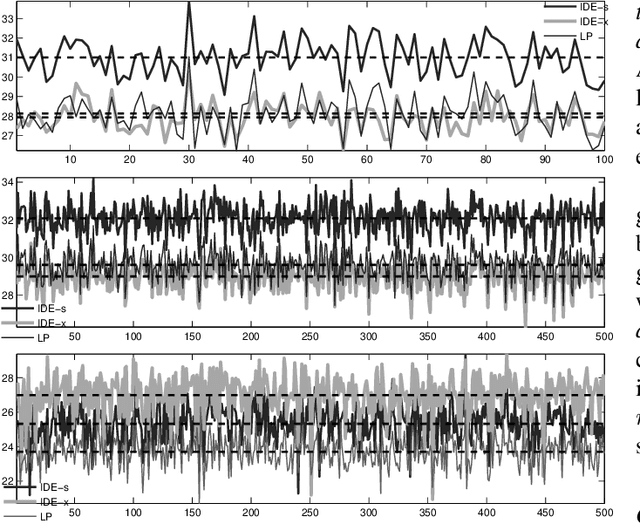
Abstract:Finding sparse solutions of underdetermined systems of linear equations is a fundamental problem in signal processing and statistics which has become a subject of interest in recent years. In general, these systems have infinitely many solutions. However, it may be shown that sufficiently sparse solutions may be identified uniquely. In other words, the corresponding linear transformation will be invertible if we restrict its domain to sufficiently sparse vectors. This property may be used, for example, to solve the underdetermined Blind Source Separation (BSS) problem, or to find sparse representation of a signal in an `overcomplete' dictionary of primitive elements (i.e., the so-called atomic decomposition). The main drawback of current methods of finding sparse solutions is their computational complexity. In this paper, we will show that by detecting `active' components of the (potential) solution, i.e., those components having a considerable value, a framework for fast solution of the problem may be devised. The idea leads to a family of algorithms, called `Iterative Detection-Estimation (IDE)', which converge to the solution by successive detection and estimation of its active part. Comparing the performance of IDE(s) with one of the most successful method to date, which is based on Linear Programming (LP), an improvement in speed of about two to three orders of magnitude is observed.
A New Trend in Optimization on Multi Overcomplete Dictionary toward Inpainting
Dec 12, 2008


Abstract:Recently, great attention was intended toward overcomplete dictionaries and the sparse representations they can provide. In a wide variety of signal processing problems, sparsity serves a crucial property leading to high performance. Inpainting, the process of reconstructing lost or deteriorated parts of images or videos, is an interesting application which can be handled by suitably decomposition of an image through combination of overcomplete dictionaries. This paper addresses a novel technique of such a decomposition and investigate that through inpainting of images. Simulations are presented to demonstrate the validation of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge