Performance Guarantees for Schatten-$p$ Quasi-Norm Minimization in Recovery of Low-Rank Matrices
Paper and Code
Oct 26, 2014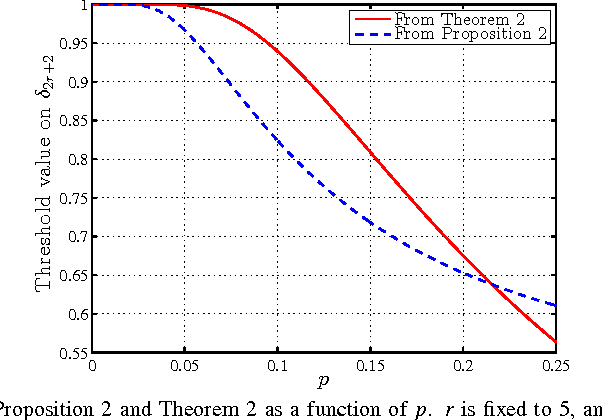
We address some theoretical guarantees for Schatten-$p$ quasi-norm minimization ($p \in (0,1]$) in recovering low-rank matrices from compressed linear measurements. Firstly, using null space properties of the measurement operator, we provide a sufficient condition for exact recovery of low-rank matrices. This condition guarantees unique recovery of matrices of ranks equal or larger than what is guaranteed by nuclear norm minimization. Secondly, this sufficient condition leads to a theorem proving that all restricted isometry property (RIP) based sufficient conditions for $\ell_p$ quasi-norm minimization generalize to Schatten-$p$ quasi-norm minimization. Based on this theorem, we provide a few RIP-based recovery conditions.
* Submitted to Elsevier Signal Processing
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge