Hanlin Yu
RVCBench: Benchmarking the Robustness of Voice Cloning Across Modern Audio Generation Models
Jan 31, 2026Abstract:Modern voice cloning (VC) can synthesize speech that closely matches a target speaker from only seconds of reference audio, enabling applications such as personalized speech interfaces and dubbing. In practical deployments, modern audio generation models inevitably encounter noisy reference audios, imperfect text prompts, and diverse downstream processing, which can significantly hurt robustness. Despite rapid progress in VC driven by autoregressive codec-token language models and diffusion-based models, robustness under realistic deployment shifts remains underexplored. This paper introduces RVCBench, a comprehensive benchmark that evaluates Robustness in VC across the full generation pipeline, including input variation, generation challenges, output post-processing, and adversarial perturbations, covering 10 robustness tasks, 225 speakers, 14,370 utterances, and 11 representative modern VC models. Our evaluation uncovers substantial robustness gaps in VC: performance can deteriorate sharply under common input shifts and post-processing; long-context and cross-lingual scenarios further expose stability limitations; and both passive noise and proactive perturbation influence generation robustness. Collectively, these findings provide a unified picture of how current VC models fail in practice and introduce a standardized, open-source testbed to support the development of more robust and deployable VC models. We open-source our project at https://github.com/Nanboy-Ronan/RVCBench.
Learning geometry and topology via multi-chart flows
May 30, 2025Abstract:Real world data often lie on low-dimensional Riemannian manifolds embedded in high-dimensional spaces. This motivates learning degenerate normalizing flows that map between the ambient space and a low-dimensional latent space. However, if the manifold has a non-trivial topology, it can never be correctly learned using a single flow. Instead multiple flows must be `glued together'. In this paper, we first propose the general training scheme for learning such a collection of flows, and secondly we develop the first numerical algorithms for computing geodesics on such manifolds. Empirically, we demonstrate that this leads to highly significant improvements in topology estimation.
Geodesic Slice Sampler for Multimodal Distributions with Strong Curvature
Feb 28, 2025Abstract:Traditional Markov Chain Monte Carlo sampling methods often struggle with sharp curvatures, intricate geometries, and multimodal distributions. Slice sampling can resolve local exploration inefficiency issues and Riemannian geometries help with sharp curvatures. Recent extensions enable slice sampling on Riemannian manifolds, but they are restricted to cases where geodesics are available in closed form. We propose a method that generalizes Hit-and-Run slice sampling to more general geometries tailored to the target distribution, by approximating geodesics as solutions to differential equations. Our approach enables exploration of regions with strong curvature and rapid transitions between modes in multimodal distributions. We demonstrate the advantages of the approach over challenging sampling problems.
Density Ratio Estimation with Conditional Probability Paths
Feb 04, 2025Abstract:Density ratio estimation in high dimensions can be reframed as integrating a certain quantity, the time score, over probability paths which interpolate between the two densities. In practice, the time score has to be estimated based on samples from the two densities. However, existing methods for this problem remain computationally expensive and can yield inaccurate estimates. Inspired by recent advances in generative modeling, we introduce a novel framework for time score estimation, based on a conditioning variable. Choosing the conditioning variable judiciously enables a closed-form objective function. We demonstrate that, compared to previous approaches, our approach results in faster learning of the time score and competitive or better estimation accuracies of the density ratio on challenging tasks. Furthermore, we establish theoretical guarantees on the error of the estimated density ratio.
Stochastic variance-reduced Gaussian variational inference on the Bures-Wasserstein manifold
Oct 03, 2024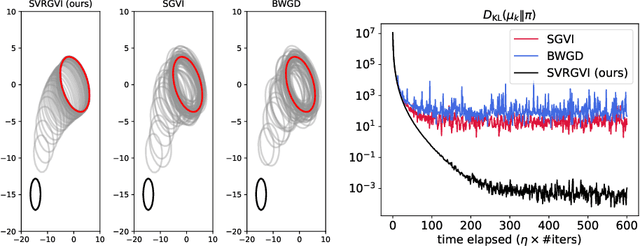
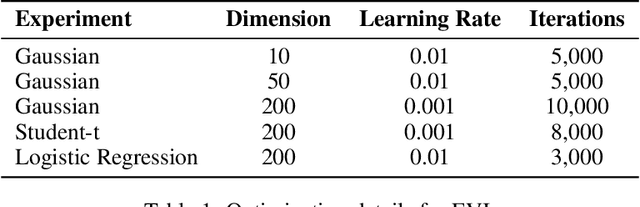
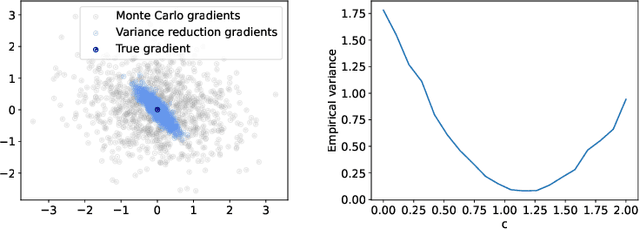
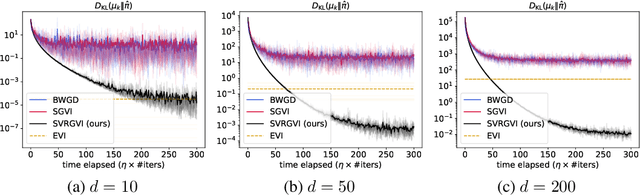
Abstract:Optimization in the Bures-Wasserstein space has been gaining popularity in the machine learning community since it draws connections between variational inference and Wasserstein gradient flows. The variational inference objective function of Kullback-Leibler divergence can be written as the sum of the negative entropy and the potential energy, making forward-backward Euler the method of choice. Notably, the backward step admits a closed-form solution in this case, facilitating the practicality of the scheme. However, the forward step is no longer exact since the Bures-Wasserstein gradient of the potential energy involves "intractable" expectations. Recent approaches propose using the Monte Carlo method -- in practice a single-sample estimator -- to approximate these terms, resulting in high variance and poor performance. We propose a novel variance-reduced estimator based on the principle of control variates. We theoretically show that this estimator has a smaller variance than the Monte-Carlo estimator in scenarios of interest. We also prove that variance reduction helps improve the optimization bounds of the current analysis. We demonstrate that the proposed estimator gains order-of-magnitude improvements over the previous Bures-Wasserstein methods.
Non-geodesically-convex optimization in the Wasserstein space
Jun 01, 2024Abstract:We study a class of optimization problems in the Wasserstein space (the space of probability measures) where the objective function is \emph{nonconvex} along generalized geodesics. When the regularization term is the negative entropy, the optimization problem becomes a sampling problem where it minimizes the Kullback-Leibler divergence between a probability measure (optimization variable) and a target probability measure whose logarithmic probability density is a nonconvex function. We derive multiple convergence insights for a novel {\em semi Forward-Backward Euler scheme} under several nonconvex (and possibly nonsmooth) regimes. Notably, the semi Forward-Backward Euler is just a slight modification of the Forward-Backward Euler whose convergence is -- to our knowledge -- still unknown in our very general non-geodesically-convex setting.
Riemannian Laplace Approximation with the Fisher Metric
Nov 08, 2023Abstract:The Laplace's method approximates a target density with a Gaussian distribution at its mode. It is computationally efficient and asymptotically exact for Bayesian inference due to the Bernstein-von Mises theorem, but for complex targets and finite-data posteriors it is often too crude an approximation. A recent generalization of the Laplace Approximation transforms the Gaussian approximation according to a chosen Riemannian geometry providing a richer approximation family, while still retaining computational efficiency. However, as shown here, its properties heavily depend on the chosen metric, indeed the metric adopted in previous work results in approximations that are overly narrow as well as being biased even at the limit of infinite data. We correct this shortcoming by developing the approximation family further, deriving two alternative variants that are exact at the limit of infinite data, extending the theoretical analysis of the method, and demonstrating practical improvements in a range of experiments.
Warped geometric information on the optimisation of Euclidean functions
Aug 16, 2023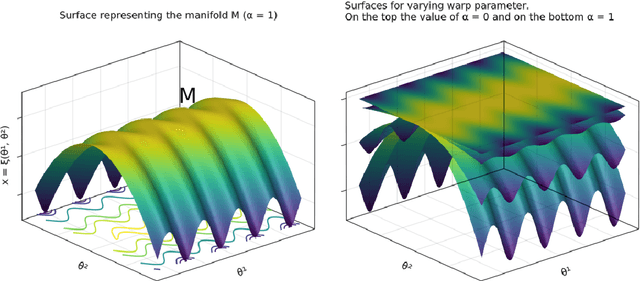
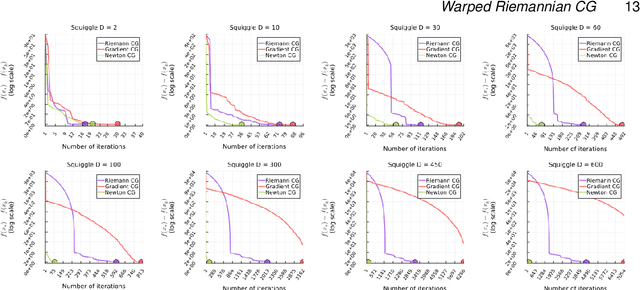
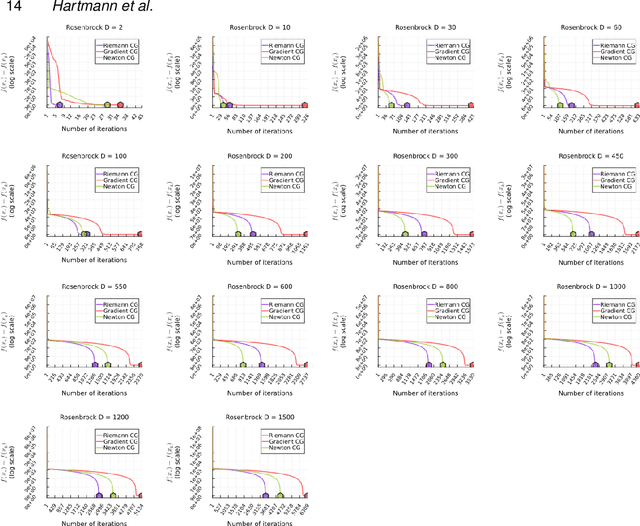
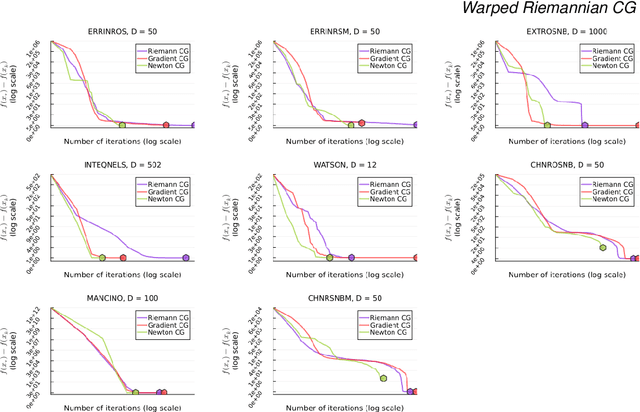
Abstract:We consider the fundamental task of optimizing a real-valued function defined in a potentially high-dimensional Euclidean space, such as the loss function in many machine-learning tasks or the logarithm of the probability distribution in statistical inference. We use the warped Riemannian geometry notions to redefine the optimisation problem of a function on Euclidean space to a Riemannian manifold with a warped metric, and then find the function's optimum along this manifold. The warped metric chosen for the search domain induces a computational friendly metric-tensor for which optimal search directions associate with geodesic curves on the manifold becomes easier to compute. Performing optimization along geodesics is known to be generally infeasible, yet we show that in this specific manifold we can analytically derive Taylor approximations up to third-order. In general these approximations to the geodesic curve will not lie on the manifold, however we construct suitable retraction maps to pull them back onto the manifold. Therefore, we can efficiently optimize along the approximate geodesic curves. We cover the related theory, describe a practical optimization algorithm and empirically evaluate it on a collection of challenging optimisation benchmarks. Our proposed algorithm, using third-order approximation of geodesics, outperforms standard Euclidean gradient-based counterparts in term of number of iterations until convergence and an alternative method for Hessian-based optimisation routines.
Scalable Stochastic Gradient Riemannian Langevin Dynamics in Non-Diagonal Metrics
Mar 09, 2023



Abstract:Bayesian neural network inference is often carried out using stochastic gradient sampling methods. For best performance the methods should use a Riemannian metric that improves posterior exploration by accounting for the local curvature, but the existing methods resort to simple diagonal metrics to remain computationally efficient. This loses some of the gains. We propose two non-diagonal metrics that can be used in stochastic samplers to improve convergence and exploration but that have only a minor computational overhead over diagonal metrics. We show that for neural networks with complex posteriors, caused e.g. by use of sparsity-inducing priors, using these metrics provides clear improvements. For some other choices the posterior is sufficiently easy also for the simpler metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge