MVICAD2: Multi-View Independent Component Analysis with Delays and Dilations

Machine learning techniques in multi-view settings face significant challenges, particularly when integrating heterogeneous data, aligning feature spaces, and managing view-specific biases. These issues are prominent in neuroscience, where data from multiple subjects exposed to the same stimuli are analyzed to uncover brain activity dynamics. In magnetoencephalography (MEG), where signals are captured at the scalp level, estimating the brain's underlying sources is crucial, especially in group studies where sources are assumed to be similar for all subjects. Common methods, such as Multi-View Independent Component Analysis (MVICA), assume identical sources across subjects, but this assumption is often too restrictive due to individual variability and age-related changes. Multi-View Independent Component Analysis with Delays (MVICAD) addresses this by allowing sources to differ up to a temporal delay. However, temporal dilation effects, particularly in auditory stimuli, are common in brain dynamics, making the estimation of time delays alone insufficient. To address this, we propose Multi-View Independent Component Analysis with Delays and Dilations (MVICAD2), which allows sources to differ across subjects in both temporal delays and dilations. We present a model with identifiable sources, derive an approximation of its likelihood in closed form, and use regularization and optimization techniques to enhance performance. Through simulations, we demonstrate that MVICAD2 outperforms existing multi-view ICA methods. We further validate its effectiveness using the Cam-CAN dataset, and showing how delays and dilations are related to aging.

Polynomial time sampling from log-smooth distributions in fixed dimension under semi-log-concavity of the forward diffusion with application to strongly dissipative distributions

In this article we provide a stochastic sampling algorithm with polynomial complexity in fixed dimension that leverages the recent advances on diffusion models where it is shown that under mild conditions, sampling can be achieved via an accurate estimation of intermediate scores across the marginals $(p_t)_{t\ge 0}$ of the standard Ornstein-Uhlenbeck process started at the density we wish to sample from. The heart of our method consists into approaching these scores via a computationally cheap estimator and relating the variance of this estimator to the smoothness properties of the forward process. Under the assumption that the density to sample from is $L$-log-smooth and that the forward process is semi-log-concave: $-\nabla^2 \log(p_t) \succeq -\beta I_d$ for some $\beta \geq 0$, we prove that our algorithm achieves an expected $\epsilon$ error in $\text{KL}$ divergence in $O(d^7L^{d+2}\epsilon^{-2(d+3)} (L+\beta)^2d^{2(d+1)})$ time. In particular, our result allows to fully transfer the problem of sampling from a log-smooth distribution into a regularity estimate problem. As an application, we derive an exponential complexity improvement for the problem of sampling from a $L$-log-smooth distribution that is $\alpha$-strongly log-concave distribution outside some ball of radius $R$: after proving that such distributions verify the semi-log-concavity assumption, a result which might be of independent interest, we recover a $poly(R,L,\alpha^{-1}, \epsilon^{-1})$ complexity in fixed dimension which exponentially improves upon the previously known $poly(e^{RL^2}, L,\alpha^{-1}, \log(\epsilon^{-1}))$ complexity in the low precision regime.

Provable Convergence and Limitations of Geometric Tempering for Langevin Dynamics

Geometric tempering is a popular approach to sampling from challenging multi-modal probability distributions by instead sampling from a sequence of distributions which interpolate, using the geometric mean, between an easier proposal distribution and the target distribution. In this paper, we theoretically investigate the soundness of this approach when the sampling algorithm is Langevin dynamics, proving both upper and lower bounds. Our upper bounds are the first analysis in the literature under functional inequalities. They assert the convergence of tempered Langevin in continuous and discrete-time, and their minimization leads to closed-form optimal tempering schedules for some pairs of proposal and target distributions. Our lower bounds demonstrate a simple case where the geometric tempering takes exponential time, and further reveal that the geometric tempering can suffer from poor functional inequalities and slow convergence, even when the target distribution is well-conditioned. Overall, our results indicate that geometric tempering may not help, and can even be harmful for convergence.

A Practical Diffusion Path for Sampling

Diffusion models are state-of-the-art methods in generative modeling when samples from a target probability distribution are available, and can be efficiently sampled, using score matching to estimate score vectors guiding a Langevin process. However, in the setting where samples from the target are not available, e.g. when this target's density is known up to a normalization constant, the score estimation task is challenging. Previous approaches rely on Monte Carlo estimators that are either computationally heavy to implement or sample-inefficient. In this work, we propose a computationally attractive alternative, relying on the so-called dilation path, that yields score vectors that are available in closed-form. This path interpolates between a Dirac and the target distribution using a convolution. We propose a simple implementation of Langevin dynamics guided by the dilation path, using adaptive step-sizes. We illustrate the results of our sampling method on a range of tasks, and shows it performs better than classical alternatives.

Provable benefits of annealing for estimating normalizing constants: Importance Sampling, Noise-Contrastive Estimation, and beyond

Recent research has developed several Monte Carlo methods for estimating the normalization constant (partition function) based on the idea of annealing. This means sampling successively from a path of distributions that interpolate between a tractable "proposal" distribution and the unnormalized "target" distribution. Prominent estimators in this family include annealed importance sampling and annealed noise-contrastive estimation (NCE). Such methods hinge on a number of design choices: which estimator to use, which path of distributions to use and whether to use a path at all; so far, there is no definitive theory on which choices are efficient. Here, we evaluate each design choice by the asymptotic estimation error it produces. First, we show that using NCE is more efficient than the importance sampling estimator, but in the limit of infinitesimal path steps, the difference vanishes. Second, we find that using the geometric path brings down the estimation error from an exponential to a polynomial function of the parameter distance between the target and proposal distributions. Third, we find that the arithmetic path, while rarely used, can offer optimality properties over the universally-used geometric path. In fact, in a particular limit, the optimal path is arithmetic. Based on this theory, we finally propose a two-step estimator to approximate the optimal path in an efficient way.

Optimizing the Noise in Self-Supervised Learning: from Importance Sampling to Noise-Contrastive Estimation

Self-supervised learning is an increasingly popular approach to unsupervised learning, achieving state-of-the-art results. A prevalent approach consists in contrasting data points and noise points within a classification task: this requires a good noise distribution which is notoriously hard to specify. While a comprehensive theory is missing, it is widely assumed that the optimal noise distribution should in practice be made equal to the data distribution, as in Generative Adversarial Networks (GANs). We here empirically and theoretically challenge this assumption. We turn to Noise-Contrastive Estimation (NCE) which grounds this self-supervised task as an estimation problem of an energy-based model of the data. This ties the optimality of the noise distribution to the sample efficiency of the estimator, which is rigorously defined as its asymptotic variance, or mean-squared error. In the special case where the normalization constant only is unknown, we show that NCE recovers a family of Importance Sampling estimators for which the optimal noise is indeed equal to the data distribution. However, in the general case where the energy is also unknown, we prove that the optimal noise density is the data density multiplied by a correction term based on the Fisher score. In particular, the optimal noise distribution is different from the data distribution, and is even from a different family. Nevertheless, we soberly conclude that the optimal noise may be hard to sample from, and the gain in efficiency can be modest compared to choosing the noise distribution equal to the data's.

The Optimal Noise in Noise-Contrastive Learning Is Not What You Think

Learning a parametric model of a data distribution is a well-known statistical problem that has seen renewed interest as it is brought to scale in deep learning. Framing the problem as a self-supervised task, where data samples are discriminated from noise samples, is at the core of state-of-the-art methods, beginning with Noise-Contrastive Estimation (NCE). Yet, such contrastive learning requires a good noise distribution, which is hard to specify; domain-specific heuristics are therefore widely used. While a comprehensive theory is missing, it is widely assumed that the optimal noise should in practice be made equal to the data, both in distribution and proportion. This setting underlies Generative Adversarial Networks (GANs) in particular. Here, we empirically and theoretically challenge this assumption on the optimal noise. We show that deviating from this assumption can actually lead to better statistical estimators, in terms of asymptotic variance. In particular, the optimal noise distribution is different from the data's and even from a different family.

Deep Recurrent Encoder: A scalable end-to-end network to model brain signals

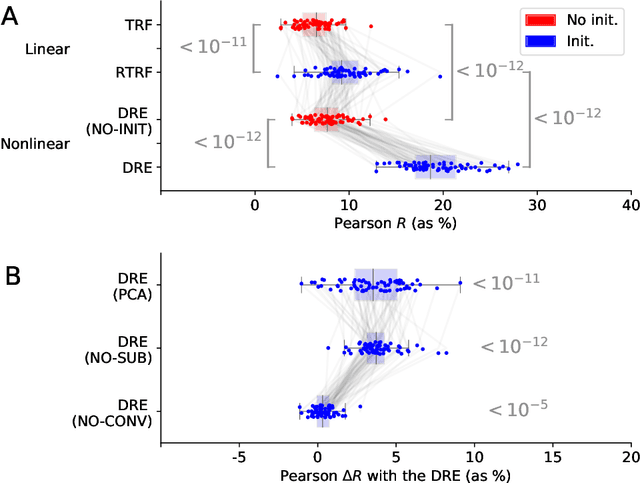
Understanding how the brain responds to sensory inputs is challenging: brain recordings are partial, noisy, and high dimensional; they vary across sessions and subjects and they capture highly nonlinear dynamics. These challenges have led the community to develop a variety of preprocessing and analytical (almost exclusively linear) methods, each designed to tackle one of these issues. Instead, we propose to address these challenges through a specific end-to-end deep learning architecture, trained to predict the brain responses of multiple subjects at once. We successfully test this approach on a large cohort of magnetoencephalography (MEG) recordings acquired during a one-hour reading task. Our Deep Recurrent Encoding (DRE) architecture reliably predicts MEG responses to words with a three-fold improvement over classic linear methods. To overcome the notorious issue of interpretability of deep learning, we describe a simple variable importance analysis. When applied to DRE, this method recovers the expected evoked responses to word length and word frequency. The quantitative improvement of the present deep learning approach paves the way to better understand the nonlinear dynamics of brain activity from large datasets.

Uncovering the structure of clinical EEG signals with self-supervised learning

Objective. Supervised learning paradigms are often limited by the amount of labeled data that is available. This phenomenon is particularly problematic in clinically-relevant data, such as electroencephalography (EEG), where labeling can be costly in terms of specialized expertise and human processing time. Consequently, deep learning architectures designed to learn on EEG data have yielded relatively shallow models and performances at best similar to those of traditional feature-based approaches. However, in most situations, unlabeled data is available in abundance. By extracting information from this unlabeled data, it might be possible to reach competitive performance with deep neural networks despite limited access to labels. Approach. We investigated self-supervised learning (SSL), a promising technique for discovering structure in unlabeled data, to learn representations of EEG signals. Specifically, we explored two tasks based on temporal context prediction as well as contrastive predictive coding on two clinically-relevant problems: EEG-based sleep staging and pathology detection. We conducted experiments on two large public datasets with thousands of recordings and performed baseline comparisons with purely supervised and hand-engineered approaches. Main results. Linear classifiers trained on SSL-learned features consistently outperformed purely supervised deep neural networks in low-labeled data regimes while reaching competitive performance when all labels were available. Additionally, the embeddings learned with each method revealed clear latent structures related to physiological and clinical phenomena, such as age effects. Significance. We demonstrate the benefit of self-supervised learning approaches on EEG data. Our results suggest that SSL may pave the way to a wider use of deep learning models on EEG data.