GRADSTOP: Early Stopping of Gradient Descent via Posterior Sampling

Machine learning models are often learned by minimising a loss function on the training data using a gradient descent algorithm. These models often suffer from overfitting, leading to a decline in predictive performance on unseen data. A standard solution is early stopping using a hold-out validation set, which halts the minimisation when the validation loss stops decreasing. However, this hold-out set reduces the data available for training. This paper presents GRADSTOP, a novel stochastic early stopping method that only uses information in the gradients, which are produced by the gradient descent algorithm ``for free.'' Our main contributions are that we estimate the Bayesian posterior by the gradient information, define the early stopping problem as drawing sample from this posterior, and use the approximated posterior to obtain a stopping criterion. Our empirical evaluation shows that GRADSTOP achieves a small loss on test data and compares favourably to a validation-set-based stopping criterion. By leveraging the entire dataset for training, our method is particularly advantageous in data-limited settings, such as transfer learning. It can be incorporated as an optional feature in gradient descent libraries with only a small computational overhead. The source code is available at https://github.com/edahelsinki/gradstop.

Geodesic Slice Sampler for Multimodal Distributions with Strong Curvature

Traditional Markov Chain Monte Carlo sampling methods often struggle with sharp curvatures, intricate geometries, and multimodal distributions. Slice sampling can resolve local exploration inefficiency issues and Riemannian geometries help with sharp curvatures. Recent extensions enable slice sampling on Riemannian manifolds, but they are restricted to cases where geodesics are available in closed form. We propose a method that generalizes Hit-and-Run slice sampling to more general geometries tailored to the target distribution, by approximating geodesics as solutions to differential equations. Our approach enables exploration of regions with strong curvature and rapid transitions between modes in multimodal distributions. We demonstrate the advantages of the approach over challenging sampling problems.

Stochastic variance-reduced Gaussian variational inference on the Bures-Wasserstein manifold

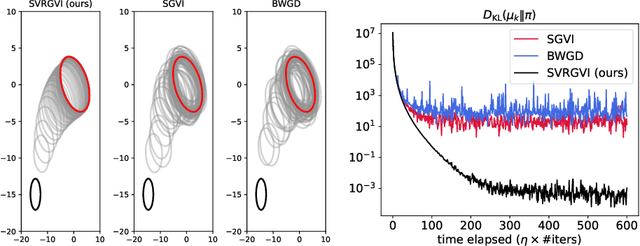
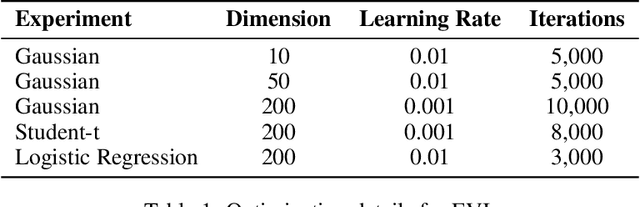
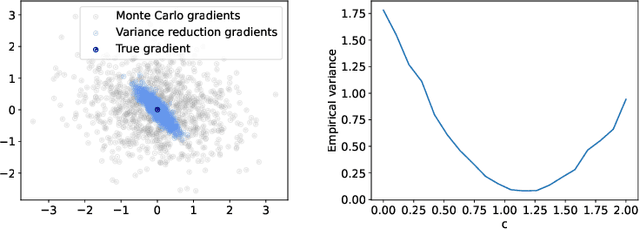
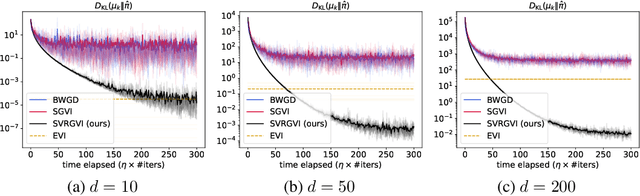
Optimization in the Bures-Wasserstein space has been gaining popularity in the machine learning community since it draws connections between variational inference and Wasserstein gradient flows. The variational inference objective function of Kullback-Leibler divergence can be written as the sum of the negative entropy and the potential energy, making forward-backward Euler the method of choice. Notably, the backward step admits a closed-form solution in this case, facilitating the practicality of the scheme. However, the forward step is no longer exact since the Bures-Wasserstein gradient of the potential energy involves "intractable" expectations. Recent approaches propose using the Monte Carlo method -- in practice a single-sample estimator -- to approximate these terms, resulting in high variance and poor performance. We propose a novel variance-reduced estimator based on the principle of control variates. We theoretically show that this estimator has a smaller variance than the Monte-Carlo estimator in scenarios of interest. We also prove that variance reduction helps improve the optimization bounds of the current analysis. We demonstrate that the proposed estimator gains order-of-magnitude improvements over the previous Bures-Wasserstein methods.

Non-geodesically-convex optimization in the Wasserstein space

We study a class of optimization problems in the Wasserstein space (the space of probability measures) where the objective function is \emph{nonconvex} along generalized geodesics. When the regularization term is the negative entropy, the optimization problem becomes a sampling problem where it minimizes the Kullback-Leibler divergence between a probability measure (optimization variable) and a target probability measure whose logarithmic probability density is a nonconvex function. We derive multiple convergence insights for a novel {\em semi Forward-Backward Euler scheme} under several nonconvex (and possibly nonsmooth) regimes. Notably, the semi Forward-Backward Euler is just a slight modification of the Forward-Backward Euler whose convergence is -- to our knowledge -- still unknown in our very general non-geodesically-convex setting.

Gradient Boosting Mapping for Dimensionality Reduction and Feature Extraction

A fundamental problem in supervised learning is to find a good set of features or distance measures. If the new set of features is of lower dimensionality and can be obtained by a simple transformation of the original data, they can make the model understandable, reduce overfitting, and even help to detect distribution drift. We propose a supervised dimensionality reduction method Gradient Boosting Mapping (GBMAP), where the outputs of weak learners -- defined as one-layer perceptrons -- define the embedding. We show that the embedding coordinates provide better features for the supervised learning task, making simple linear models competitive with the state-of-the-art regressors and classifiers. We also use the embedding to find a principled distance measure between points. The features and distance measures automatically ignore directions irrelevant to the supervised learning task. We also show that we can reliably detect out-of-distribution data points with potentially large regression or classification errors. GBMAP is fast and works in seconds for dataset of million data points or hundreds of features. As a bonus, GBMAP provides a regression and classification performance comparable to the state-of-the-art supervised learning methods.