Minimum Stein Discrepancy Estimators

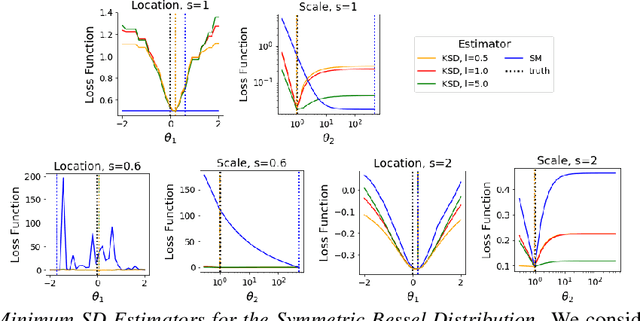
When maximum likelihood estimation is infeasible, one often turns to score matching, contrastive divergence, or minimum probability flow learning to obtain tractable parameter estimates. We provide a unifying perspective of these techniques as minimum Stein discrepancy estimators and use this lens to design new diffusion kernel Stein discrepancy (DKSD) and diffusion score matching (DSM) estimators with complementary strengths. We establish the consistency, asymptotic normality, and robustness of DKSD and DSM estimators, derive stochastic Riemannian gradient descent algorithms for their efficient optimization, and demonstrate their advantages over score matching in models with non-smooth densities or heavy tailed distributions.