Contributed Discussion of "A Bayesian Conjugate Gradient Method"

We would like to congratulate the authors of "A Bayesian Conjugate Gradient Method" on their insightful paper, and welcome this publication which we firmly believe will become a fundamental contribution to the growing field of probabilistic numerical methods and in particular the sub-field of Bayesian numerical methods. In this short piece, which will be published as a comment alongside the main paper, we first initiate a discussion on the choice of priors for solving linear systems, then propose an extension of the Bayesian conjugate gradient (BayesCG) algorithm for solving several related linear systems simultaneously.

Minimum Stein Discrepancy Estimators

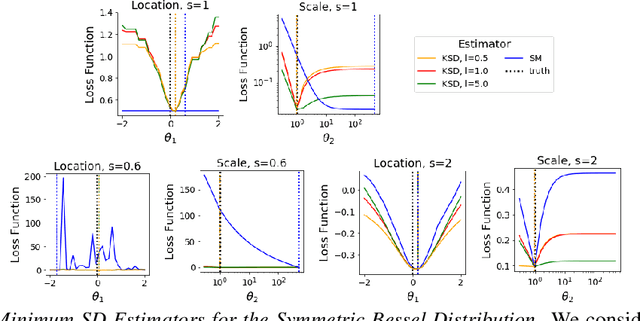
When maximum likelihood estimation is infeasible, one often turns to score matching, contrastive divergence, or minimum probability flow learning to obtain tractable parameter estimates. We provide a unifying perspective of these techniques as minimum Stein discrepancy estimators and use this lens to design new diffusion kernel Stein discrepancy (DKSD) and diffusion score matching (DSM) estimators with complementary strengths. We establish the consistency, asymptotic normality, and robustness of DKSD and DSM estimators, derive stochastic Riemannian gradient descent algorithms for their efficient optimization, and demonstrate their advantages over score matching in models with non-smooth densities or heavy tailed distributions.

Statistical Inference for Generative Models with Maximum Mean Discrepancy

While likelihood-based inference and its variants provide a statistically efficient and widely applicable approach to parametric inference, their application to models involving intractable likelihoods poses challenges. In this work, we study a class of minimum distance estimators for intractable generative models, that is, statistical models for which the likelihood is intractable, but simulation is cheap. The distance considered, maximum mean discrepancy (MMD), is defined through the embedding of probability measures into a reproducing kernel Hilbert space. We study the theoretical properties of these estimators, showing that they are consistent, asymptotically normal and robust to model misspecification. A main advantage of these estimators is the flexibility offered by the choice of kernel, which can be used to trade-off statistical efficiency and robustness. On the algorithmic side, we study the geometry induced by MMD on the parameter space and use this to introduce a novel natural gradient descent-like algorithm for efficient implementation of these estimators. We illustrate the relevance of our theoretical results on several classes of models including a discrete-time latent Markov process and two multivariate stochastic differential equation models.

Rejoinder for "Probabilistic Integration: A Role in Statistical Computation?"

This article is the rejoinder for the paper "Probabilistic Integration: A Role in Statistical Computation?" to appear in Statistical Science with discussion. We would first like to thank the reviewers and many of our colleagues who helped shape this paper, the editor for selecting our paper for discussion, and of course all of the discussants for their thoughtful, insightful and constructive comments. In this rejoinder, we respond to some of the points raised by the discussants and comment further on the fundamental questions underlying the paper: (i) Should Bayesian ideas be used in numerical analysis?, and (ii) If so, what role should such approaches have in statistical computation?

On the Sampling Problem for Kernel Quadrature

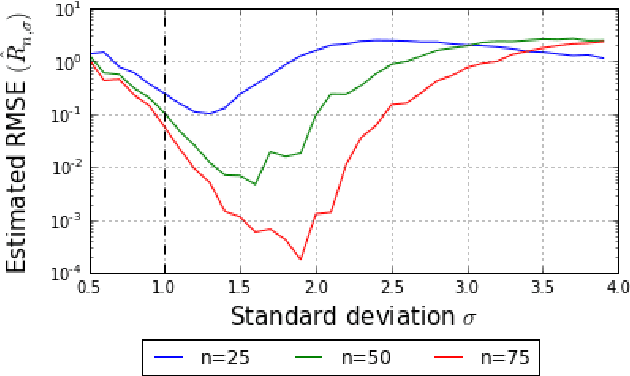
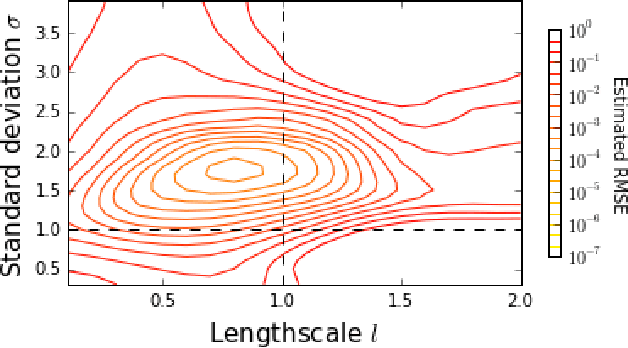
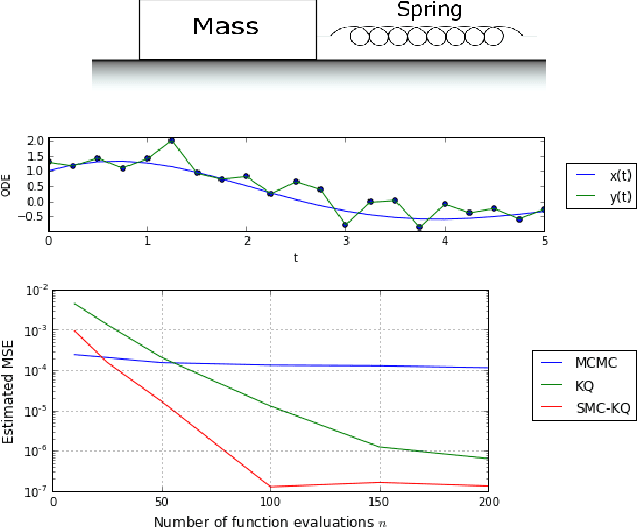
The standard Kernel Quadrature method for numerical integration with random point sets (also called Bayesian Monte Carlo) is known to converge in root mean square error at a rate determined by the ratio $s/d$, where $s$ and $d$ encode the smoothness and dimension of the integrand. However, an empirical investigation reveals that the rate constant $C$ is highly sensitive to the distribution of the random points. In contrast to standard Monte Carlo integration, for which optimal importance sampling is well-understood, the sampling distribution that minimises $C$ for Kernel Quadrature does not admit a closed form. This paper argues that the practical choice of sampling distribution is an important open problem. One solution is considered; a novel automatic approach based on adaptive tempering and sequential Monte Carlo. Empirical results demonstrate a dramatic reduction in integration error of up to 4 orders of magnitude can be achieved with the proposed method.

Geometry and Dynamics for Markov Chain Monte Carlo

Markov Chain Monte Carlo methods have revolutionised mathematical computation and enabled statistical inference within many previously intractable models. In this context, Hamiltonian dynamics have been proposed as an efficient way of building chains which can explore probability densities efficiently. The method emerges from physics and geometry and these links have been extensively studied by a series of authors through the last thirty years. However, there is currently a gap between the intuitions and knowledge of users of the methodology and our deep understanding of these theoretical foundations. The aim of this review is to provide a comprehensive introduction to the geometric tools used in Hamiltonian Monte Carlo at a level accessible to statisticians, machine learners and other users of the methodology with only a basic understanding of Monte Carlo methods. This will be complemented with some discussion of the most recent advances in the field which we believe will become increasingly relevant to applied scientists.