Stein Point Markov Chain Monte Carlo

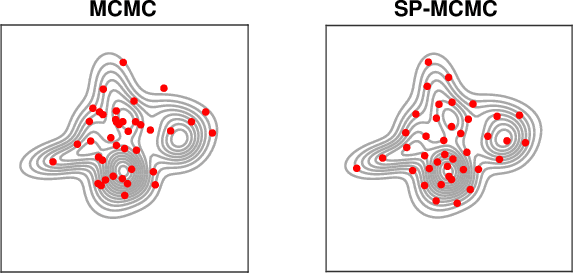
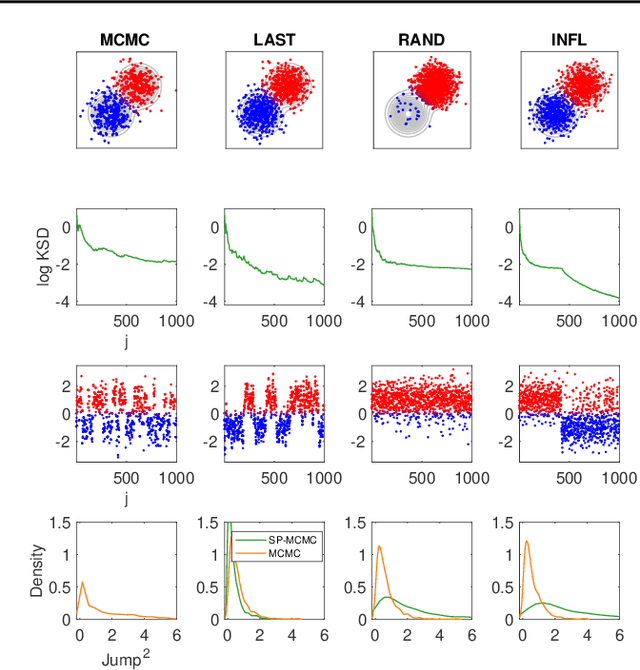
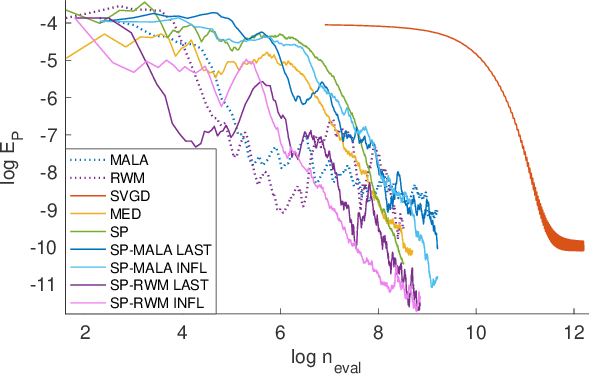
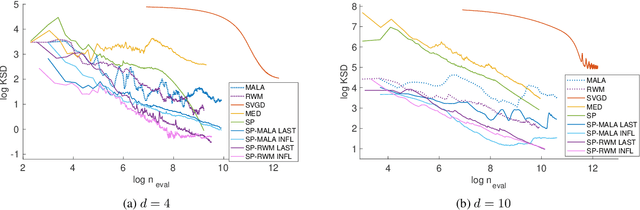
An important task in machine learning and statistics is the approximation of a probability measure by an empirical measure supported on a discrete point set. Stein Points are a class of algorithms for this task, which proceed by sequentially minimising a Stein discrepancy between the empirical measure and the target and, hence, require the solution of a non-convex optimisation problem to obtain each new point. This paper removes the need to solve this optimisation problem by, instead, selecting each new point based on a Markov chain sample path. This significantly reduces the computational cost of Stein Points and leads to a suite of algorithms that are straightforward to implement. The new algorithms are illustrated on a set of challenging Bayesian inference problems, and rigorous theoretical guarantees of consistency are established.

Stein Points

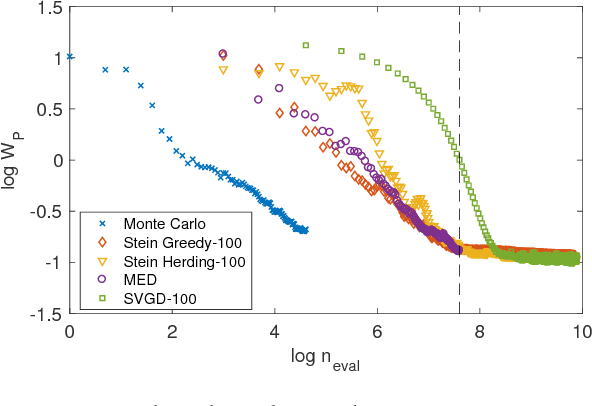
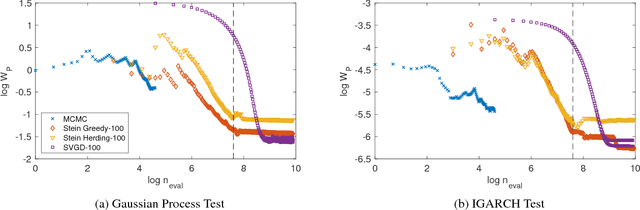
An important task in computational statistics and machine learning is to approximate a posterior distribution $p(x)$ with an empirical measure supported on a set of representative points $\{x_i\}_{i=1}^n$. This paper focuses on methods where the selection of points is essentially deterministic, with an emphasis on achieving accurate approximation when $n$ is small. To this end, we present `Stein Points'. The idea is to exploit either a greedy or a conditional gradient method to iteratively minimise a kernel Stein discrepancy between the empirical measure and $p(x)$. Our empirical results demonstrate that Stein Points enable accurate approximation of the posterior at modest computational cost. In addition, theoretical results are provided to establish convergence of the method.

On the Sampling Problem for Kernel Quadrature

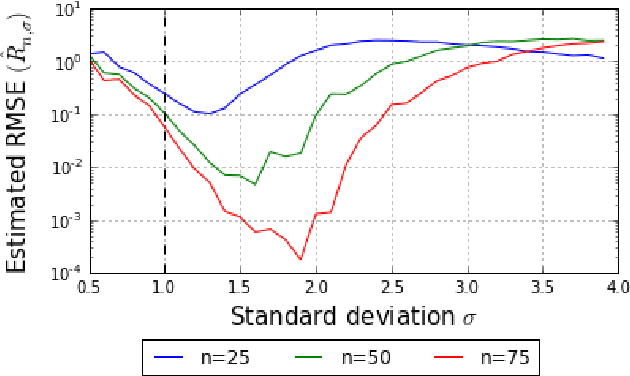
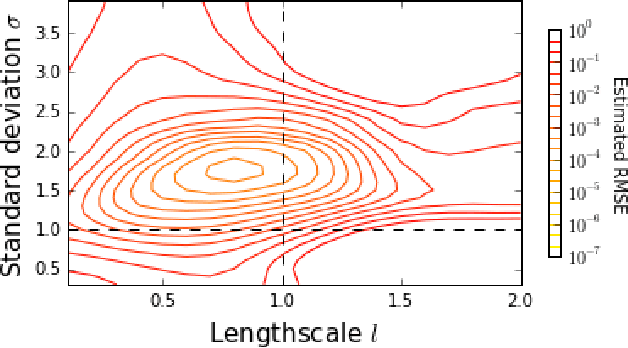
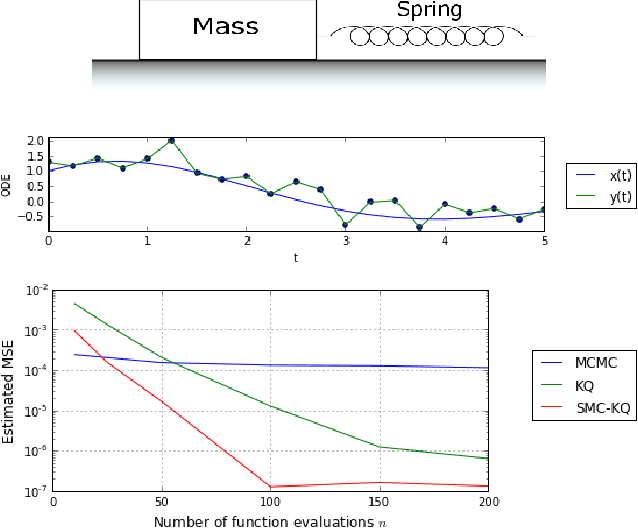
The standard Kernel Quadrature method for numerical integration with random point sets (also called Bayesian Monte Carlo) is known to converge in root mean square error at a rate determined by the ratio $s/d$, where $s$ and $d$ encode the smoothness and dimension of the integrand. However, an empirical investigation reveals that the rate constant $C$ is highly sensitive to the distribution of the random points. In contrast to standard Monte Carlo integration, for which optimal importance sampling is well-understood, the sampling distribution that minimises $C$ for Kernel Quadrature does not admit a closed form. This paper argues that the practical choice of sampling distribution is an important open problem. One solution is considered; a novel automatic approach based on adaptive tempering and sequential Monte Carlo. Empirical results demonstrate a dramatic reduction in integration error of up to 4 orders of magnitude can be achieved with the proposed method.