A Unifying and Canonical Description of Measure-Preserving Diffusions

A complete recipe of measure-preserving diffusions in Euclidean space was recently derived unifying several MCMC algorithms into a single framework. In this paper, we develop a geometric theory that improves and generalises this construction to any manifold. We thereby demonstrate that the completeness result is a direct consequence of the topology of the underlying manifold and the geometry induced by the target measure $P$; there is no need to introduce other structures such as a Riemannian metric, local coordinates, or a reference measure. Instead, our framework relies on the intrinsic geometry of $P$ and in particular its canonical derivative, the deRham rotationnel, which allows us to parametrise the Fokker--Planck currents of measure-preserving diffusions using potentials. The geometric formalism can easily incorporate constraints and symmetries, and deliver new important insights, for example, a new complete recipe of Langevin-like diffusions that are suited to the construction of samplers. We also analyse the reversibility and dissipative properties of the diffusions, the associated deterministic flow on the space of measures, and the geometry of Langevin processes. Our article connects ideas from various literature and frames the theory of measure-preserving diffusions in its appropriate mathematical context.

Optimization algorithms inspired by the geometry of dissipative systems

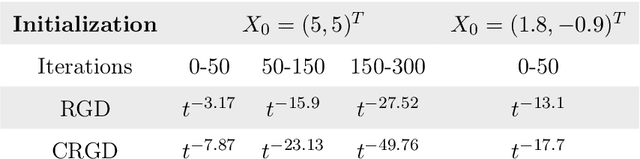
Accelerated gradient methods are a powerful optimization tool in machine learning and statistics but their development has traditionally been driven by heuristic motivations. Recent research, however, has demonstrated that these methods can be derived as discretizations of dynamical systems, which in turn has provided a basis for more systematic investigations, especially into the structure of those dynamical systems and their structure preserving discretizations. In this work we introduce dynamical systems defined through a contact geometry which are not only naturally suited to the optimization goal but also subsume all previous methods based on geometric dynamical systems. These contact dynamical systems also admit a natural, robust discretization through geometric contact integrators. We demonstrate these features in paradigmatic examples which show that we can indeed obtain optimization algorithms that achieve oracle lower bounds on convergence rates while also improving on previous proposals in terms of stability.

On the Geometric Ergodicity of Hamiltonian Monte Carlo

We establish general conditions under which Markov chains produced by the Hamiltonian Monte Carlo method will and will not be geometrically ergodic. We consider implementations with both position-independent and position-dependent integration times. In the former case we find that the conditions for geometric ergodicity are essentially a non-vanishing gradient of the log-density which asymptotically points towards the centre of the space and does not grow faster than linearly. In an idealised scenario in which the integration time is allowed to change in different regions of the space, we show that geometric ergodicity can be recovered for a much broader class of tail behaviours, leading to some guidelines for the choice of this free parameter in practice.