Musical Stylistic Analysis: A Study of Intervallic Transition Graphs via Persistent Homology

Topological data analysis has been recently applied to investigate stylistic signatures and trends in musical compositions. A useful tool in this area is Persistent Homology. In this paper, we develop a novel method to represent a weighted directed graph as a finite metric space and then use persistent homology to extract useful features. We apply this method to weighted directed graphs obtained from pitch transitions information of a given musical fragment and use these techniques to the study of stylistic trends. In particular, we are interested in using these tools to make quantitative stylistic comparisons. As a first illustration, we analyze a selection of string quartets by Haydn, Mozart and Beethoven and discuss possible implications of our results in terms of different approaches by these composers to stylistic exploration and variety. We observe that Haydn is stylistically the most conservative, followed by Mozart, while Beethoven is the most innovative, expanding and modifying the string quartet as a musical form. Finally we also compare the variability of different genres, namely minuets, allegros, prestos and adagios, by a given composer and conclude that the minuet is the most stable form of the string quartet movements.

Optimization algorithms inspired by the geometry of dissipative systems

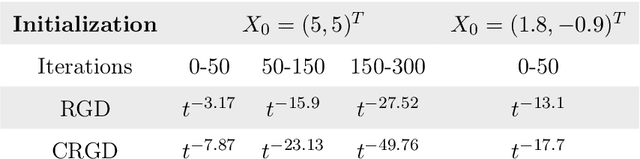
Accelerated gradient methods are a powerful optimization tool in machine learning and statistics but their development has traditionally been driven by heuristic motivations. Recent research, however, has demonstrated that these methods can be derived as discretizations of dynamical systems, which in turn has provided a basis for more systematic investigations, especially into the structure of those dynamical systems and their structure preserving discretizations. In this work we introduce dynamical systems defined through a contact geometry which are not only naturally suited to the optimization goal but also subsume all previous methods based on geometric dynamical systems. These contact dynamical systems also admit a natural, robust discretization through geometric contact integrators. We demonstrate these features in paradigmatic examples which show that we can indeed obtain optimization algorithms that achieve oracle lower bounds on convergence rates while also improving on previous proposals in terms of stability.