Learning Dynamic Tasks on a Large-scale Soft Robot in a Handful of Trials

Soft robots offer more flexibility, compliance, and adaptability than traditional rigid robots. They are also typically lighter and cheaper to manufacture. However, their use in real-world applications is limited due to modeling challenges and difficulties in integrating effective proprioceptive sensors. Large-scale soft robots ($\approx$ two meters in length) have greater modeling complexity due to increased inertia and related effects of gravity. Common efforts to ease these modeling difficulties such as assuming simple kinematic and dynamics models also limit the general capabilities of soft robots and are not applicable in tasks requiring fast, dynamic motion like throwing and hammering. To overcome these challenges, we propose a data-efficient Bayesian optimization-based approach for learning control policies for dynamic tasks on a large-scale soft robot. Our approach optimizes the task objective function directly from commanded pressures, without requiring approximate kinematics or dynamics as an intermediate step. We demonstrate the effectiveness of our approach through both simulated and real-world experiments.

One Initialization to Rule them All: Fine-tuning via Explained Variance Adaptation

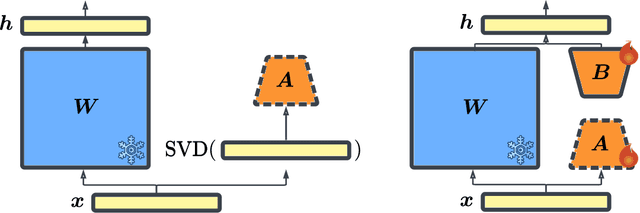
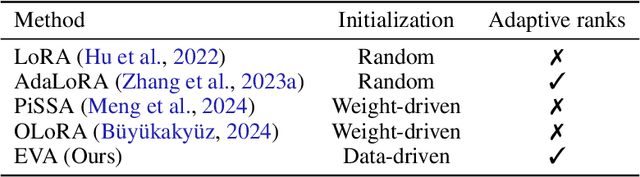
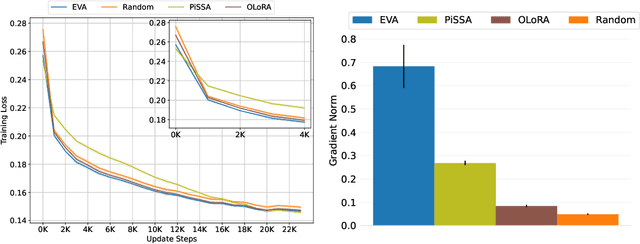
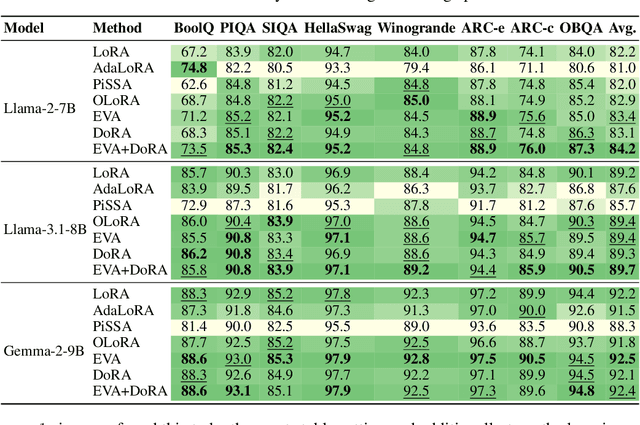
Foundation models (FMs) are pre-trained on large-scale datasets and then fine-tuned on a downstream task for a specific application. The most successful and most commonly used fine-tuning method is to update the pre-trained weights via a low-rank adaptation (LoRA). LoRA introduces new weight matrices that are usually initialized at random with a uniform rank distribution across model weights. Recent works focus on weight-driven initialization or learning of adaptive ranks during training. Both approaches have only been investigated in isolation, resulting in slow convergence or a uniform rank distribution, in turn leading to sub-optimal performance. We propose to enhance LoRA by initializing the new weights in a data-driven manner by computing singular value decomposition on minibatches of activation vectors. Then, we initialize the LoRA matrices with the obtained right-singular vectors and re-distribute ranks among all weight matrices to explain the maximal amount of variance and continue the standard LoRA fine-tuning procedure. This results in our new method Explained Variance Adaptation (EVA). We apply EVA to a variety of fine-tuning tasks ranging from language generation and understanding to image classification and reinforcement learning. EVA exhibits faster convergence than competitors and attains the highest average score across a multitude of tasks per domain.

Uncertainty Quantification of Pre-Trained and Fine-Tuned Surrogate Models using Conformal Prediction

Data-driven surrogate models have shown immense potential as quick, inexpensive approximations to complex numerical and experimental modelling tasks. However, most surrogate models characterising physical systems do not quantify their uncertainty, rendering their predictions unreliable, and needing further validation. Though Bayesian approximations offer some solace in estimating the error associated with these models, they cannot provide they cannot provide guarantees, and the quality of their inferences depends on the availability of prior information and good approximations to posteriors for complex problems. This is particularly pertinent to multi-variable or spatio-temporal problems. Our work constructs and formalises a conformal prediction framework that satisfies marginal coverage for spatio-temporal predictions in a model-agnostic manner, requiring near-zero computational costs. The paper provides an extensive empirical study of the application of the framework to ascertain valid error bars that provide guaranteed coverage across the surrogate model's domain of operation. The application scope of our work extends across a large range of spatio-temporal models, ranging from solving partial differential equations to weather forecasting. Through the applications, the paper looks at providing statistically valid error bars for deterministic models, as well as crafting guarantees to the error bars of probabilistic models. The paper concludes with a viable conformal prediction formalisation that provides guaranteed coverage of the surrogate model, regardless of model architecture, and its training regime and is unbothered by the curse of dimensionality.

Reparameterized Multi-Resolution Convolutions for Long Sequence Modelling

Global convolutions have shown increasing promise as powerful general-purpose sequence models. However, training long convolutions is challenging, and kernel parameterizations must be able to learn long-range dependencies without overfitting. This work introduces reparameterized multi-resolution convolutions ($\texttt{MRConv}$), a novel approach to parameterizing global convolutional kernels for long-sequence modelling. By leveraging multi-resolution convolutions, incorporating structural reparameterization and introducing learnable kernel decay, $\texttt{MRConv}$ learns expressive long-range kernels that perform well across various data modalities. Our experiments demonstrate state-of-the-art performance on the Long Range Arena, Sequential CIFAR, and Speech Commands tasks among convolution models and linear-time transformers. Moreover, we report improved performance on ImageNet classification by replacing 2D convolutions with 1D $\texttt{MRConv}$ layers.

Probabilistic Weather Forecasting with Hierarchical Graph Neural Networks

In recent years, machine learning has established itself as a powerful tool for high-resolution weather forecasting. While most current machine learning models focus on deterministic forecasts, accurately capturing the uncertainty in the chaotic weather system calls for probabilistic modeling. We propose a probabilistic weather forecasting model called Graph-EFM, combining a flexible latent-variable formulation with the successful graph-based forecasting framework. The use of a hierarchical graph construction allows for efficient sampling of spatially coherent forecasts. Requiring only a single forward pass per time step, Graph-EFM allows for fast generation of arbitrarily large ensembles. We experiment with the model on both global and limited area forecasting. Ensemble forecasts from Graph-EFM achieve equivalent or lower errors than comparable deterministic models, with the added benefit of accurately capturing forecast uncertainty.

Scalable Data Assimilation with Message Passing

Data assimilation is a core component of numerical weather prediction systems. The large quantity of data processed during assimilation requires the computation to be distributed across increasingly many compute nodes, yet existing approaches suffer from synchronisation overhead in this setting. In this paper, we exploit the formulation of data assimilation as a Bayesian inference problem and apply a message-passing algorithm to solve the spatial inference problem. Since message passing is inherently based on local computations, this approach lends itself to parallel and distributed computation. In combination with a GPU-accelerated implementation, we can scale the algorithm to very large grid sizes while retaining good accuracy and compute and memory requirements.

Iterated INLA for State and Parameter Estimation in Nonlinear Dynamical Systems

Data assimilation (DA) methods use priors arising from differential equations to robustly interpolate and extrapolate data. Popular techniques such as ensemble methods that handle high-dimensional, nonlinear PDE priors focus mostly on state estimation, however can have difficulty learning the parameters accurately. On the other hand, machine learning based approaches can naturally learn the state and parameters, but their applicability can be limited, or produce uncertainties that are hard to interpret. Inspired by the Integrated Nested Laplace Approximation (INLA) method in spatial statistics, we propose an alternative approach to DA based on iteratively linearising the dynamical model. This produces a Gaussian Markov random field at each iteration, enabling one to use INLA to infer the state and parameters. Our approach can be used for arbitrary nonlinear systems, while retaining interpretability, and is furthermore demonstrated to outperform existing methods on the DA task. By providing a more nuanced approach to handling nonlinear PDE priors, our methodology offers improved accuracy and robustness in predictions, especially where data sparsity is prevalent.

Plasma Surrogate Modelling using Fourier Neural Operators

Predicting plasma evolution within a Tokamak reactor is crucial to realizing the goal of sustainable fusion. Capabilities in forecasting the spatio-temporal evolution of plasma rapidly and accurately allow us to quickly iterate over design and control strategies on current Tokamak devices and future reactors. Modelling plasma evolution using numerical solvers is often expensive, consuming many hours on supercomputers, and hence, we need alternative inexpensive surrogate models. We demonstrate accurate predictions of plasma evolution both in simulation and experimental domains using deep learning-based surrogate modelling tools, viz., Fourier Neural Operators (FNO). We show that FNO has a speedup of six orders of magnitude over traditional solvers in predicting the plasma dynamics simulated from magnetohydrodynamic models, while maintaining a high accuracy (MSE $\approx$ $10^{-5}$). Our modified version of the FNO is capable of solving multi-variable Partial Differential Equations (PDE), and can capture the dependence among the different variables in a single model. FNOs can also predict plasma evolution on real-world experimental data observed by the cameras positioned within the MAST Tokamak, i.e., cameras looking across the central solenoid and the divertor in the Tokamak. We show that FNOs are able to accurately forecast the evolution of plasma and have the potential to be deployed for real-time monitoring. We also illustrate their capability in forecasting the plasma shape, the locations of interactions of the plasma with the central solenoid and the divertor for the full duration of the plasma shot within MAST. The FNO offers a viable alternative for surrogate modelling as it is quick to train and infer, and requires fewer data points, while being able to do zero-shot super-resolution and getting high-fidelity solutions.

Gaussian Processes on Cellular Complexes

In recent years, there has been considerable interest in developing machine learning models on graphs in order to account for topological inductive biases. In particular, recent attention was given to Gaussian processes on such structures since they can additionally account for uncertainty. However, graphs are limited to modelling relations between two vertices. In this paper, we go beyond this dyadic setting and consider polyadic relations that include interactions between vertices, edges and one of their generalisations, known as cells. Specifically, we propose Gaussian processes on cellular complexes, a generalisation of graphs that captures interactions between these higher-order cells. One of our key contributions is the derivation of two novel kernels, one that generalises the graph Mat\'ern kernel and one that additionally mixes information of different cell types.

Thin and Deep Gaussian Processes

Gaussian processes (GPs) can provide a principled approach to uncertainty quantification with easy-to-interpret kernel hyperparameters, such as the lengthscale, which controls the correlation distance of function values. However, selecting an appropriate kernel can be challenging. Deep GPs avoid manual kernel engineering by successively parameterizing kernels with GP layers, allowing them to learn low-dimensional embeddings of the inputs that explain the output data. Following the architecture of deep neural networks, the most common deep GPs warp the input space layer-by-layer but lose all the interpretability of shallow GPs. An alternative construction is to successively parameterize the lengthscale of a kernel, improving the interpretability but ultimately giving away the notion of learning lower-dimensional embeddings. Unfortunately, both methods are susceptible to particular pathologies which may hinder fitting and limit their interpretability. This work proposes a novel synthesis of both previous approaches: Thin and Deep GP (TDGP). Each TDGP layer defines locally linear transformations of the original input data maintaining the concept of latent embeddings while also retaining the interpretation of lengthscales of a kernel. Moreover, unlike the prior solutions, TDGP induces non-pathological manifolds that admit learning lower-dimensional representations. We show with theoretical and experimental results that i) TDGP is, unlike previous models, tailored to specifically discover lower-dimensional manifolds in the input data, ii) TDGP behaves well when increasing the number of layers, and iii) TDGP performs well in standard benchmark datasets.