Thin and Deep Gaussian Processes

Gaussian processes (GPs) can provide a principled approach to uncertainty quantification with easy-to-interpret kernel hyperparameters, such as the lengthscale, which controls the correlation distance of function values. However, selecting an appropriate kernel can be challenging. Deep GPs avoid manual kernel engineering by successively parameterizing kernels with GP layers, allowing them to learn low-dimensional embeddings of the inputs that explain the output data. Following the architecture of deep neural networks, the most common deep GPs warp the input space layer-by-layer but lose all the interpretability of shallow GPs. An alternative construction is to successively parameterize the lengthscale of a kernel, improving the interpretability but ultimately giving away the notion of learning lower-dimensional embeddings. Unfortunately, both methods are susceptible to particular pathologies which may hinder fitting and limit their interpretability. This work proposes a novel synthesis of both previous approaches: Thin and Deep GP (TDGP). Each TDGP layer defines locally linear transformations of the original input data maintaining the concept of latent embeddings while also retaining the interpretation of lengthscales of a kernel. Moreover, unlike the prior solutions, TDGP induces non-pathological manifolds that admit learning lower-dimensional representations. We show with theoretical and experimental results that i) TDGP is, unlike previous models, tailored to specifically discover lower-dimensional manifolds in the input data, ii) TDGP behaves well when increasing the number of layers, and iii) TDGP performs well in standard benchmark datasets.

Learning Energy Conserving Dynamics Efficiently with Hamiltonian Gaussian Processes

Hamiltonian mechanics is one of the cornerstones of natural sciences. Recently there has been significant interest in learning Hamiltonian systems in a free-form way directly from trajectory data. Previous methods have tackled the problem of learning from many short, low-noise trajectories, but learning from a small number of long, noisy trajectories, whilst accounting for model uncertainty has not been addressed. In this work, we present a Gaussian process model for Hamiltonian systems with efficient decoupled parameterisation, and introduce an energy-conserving shooting method that allows robust inference from both short and long trajectories. We demonstrate the method's success in learning Hamiltonian systems in various data settings.

Shallow and Deep Nonparametric Convolutions for Gaussian Processes

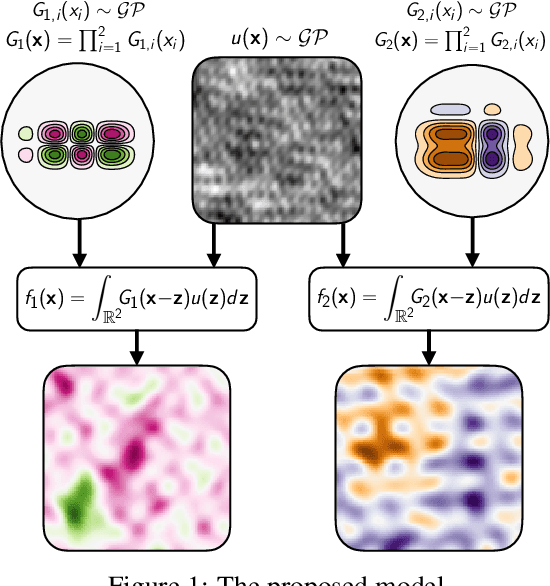
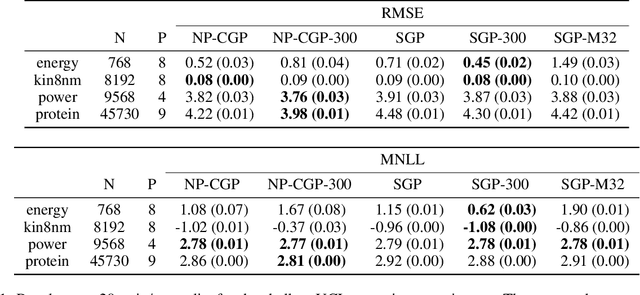
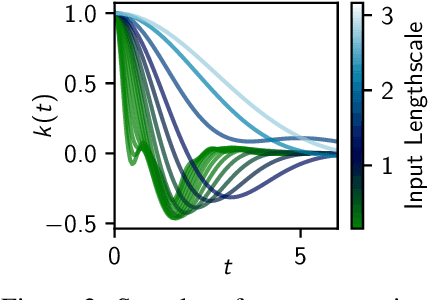
A key challenge in the practical application of Gaussian processes (GPs) is selecting a proper covariance function. The moving average, or process convolutions, construction of GPs allows some additional flexibility, but still requires choosing a proper smoothing kernel, which is non-trivial. Previous approaches have built covariance functions by using GP priors over the smoothing kernel, and by extension the covariance, as a way to bypass the need to specify it in advance. However, such models have been limited in several ways: they are restricted to single dimensional inputs, e.g. time; they only allow modelling of single outputs and they do not scale to large datasets since inference is not straightforward. In this paper, we introduce a nonparametric process convolution formulation for GPs that alleviates these weaknesses by using a functional sampling approach based on Matheron's rule to perform fast sampling using interdomain inducing variables. Furthermore, we propose a composition of these nonparametric convolutions that serves as an alternative to classic deep GP models, and allows the covariance functions of the intermediate layers to be inferred from the data. We test the performance of our model on benchmarks for single output GPs, multiple output GPs and deep GPs and find that in many cases our approach can provide improvements over standard GP models.

Modelling calibration uncertainty in networks of environmental sensors

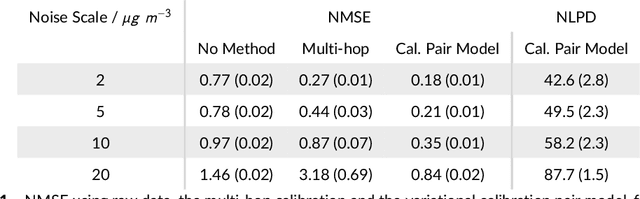
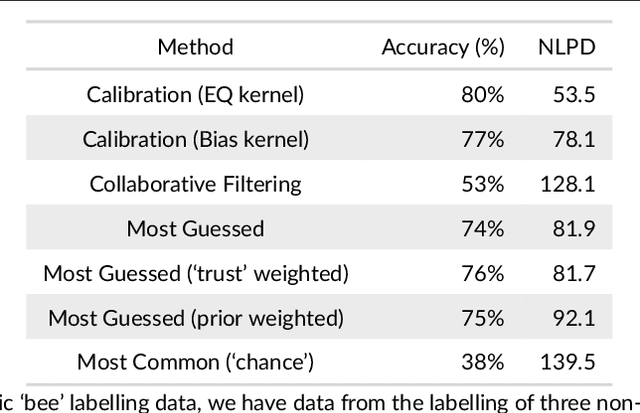
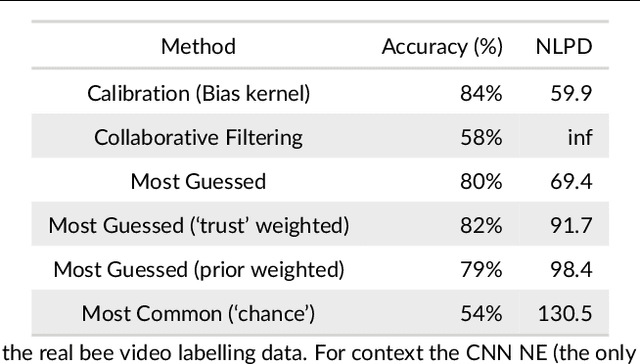
Networks of low-cost sensors are becoming ubiquitous, but often suffer from poor accuracies and drift. Regular colocation with reference sensors allows recalibration but is complicated and expensive. Alternatively the calibration can be transferred using low-cost, mobile sensors. However inferring the calibration (with uncertainty) becomes difficult. We propose a variational approach to model the calibration across the network. We demonstrate the approach on synthetic and real air pollution data, and find it can perform better than the state of the art (multi-hop calibration). We extend it to categorical data produced by citizen-scientist labelling. In Summary: The method achieves uncertainty-quantified calibration, which has been one of the barriers to low-cost sensor deployment and citizen-science research.

Learning Nonparametric Volterra Kernels with Gaussian Processes

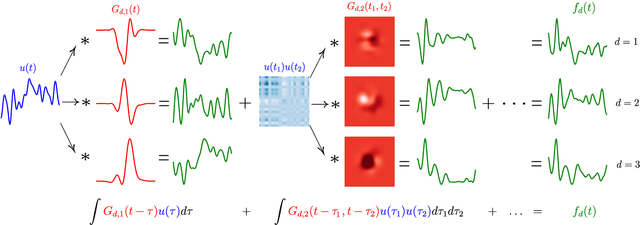
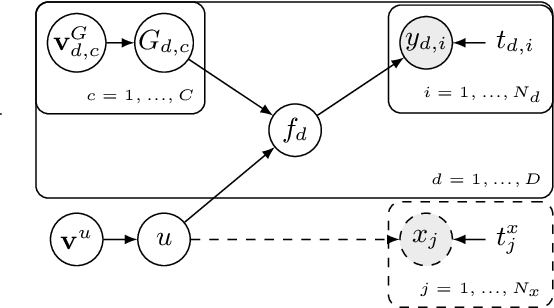
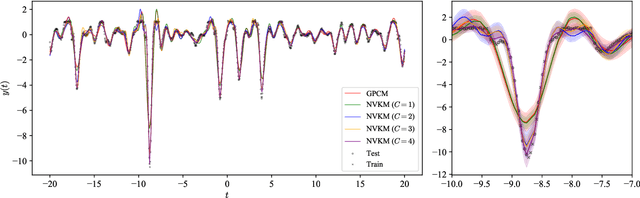
This paper introduces a method for the nonparametric Bayesian learning of nonlinear operators, through the use of the Volterra series with kernels represented using Gaussian processes (GPs), which we term the nonparametric Volterra kernels model (NVKM). When the input function to the operator is unobserved and has a GP prior, the NVKM constitutes a powerful method for both single and multiple output regression, and can be viewed as a nonlinear and nonparametric latent force model. When the input function is observed, the NVKM can be used to perform Bayesian system identification. We use recent advances in efficient sampling of explicit functions from GPs to map process realisations through the Volterra series without resorting to numerical integration, allowing scalability through doubly stochastic variational inference, and avoiding the need for Gaussian approximations of the output processes. We demonstrate the performance of the model for both multiple output regression and system identification using standard benchmarks.