Gaussian Processes for Monitoring Air-Quality in Kampala

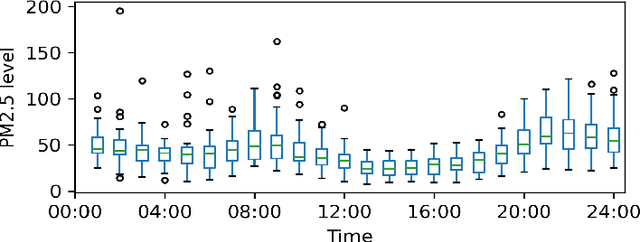
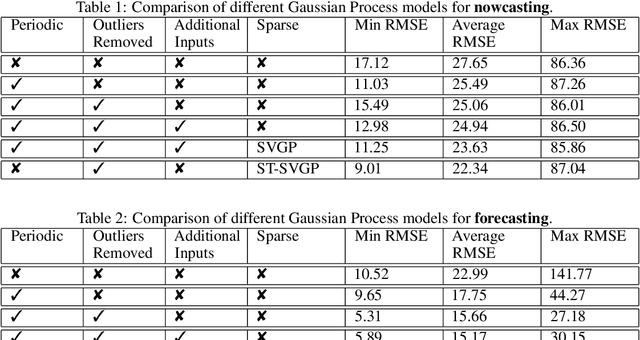
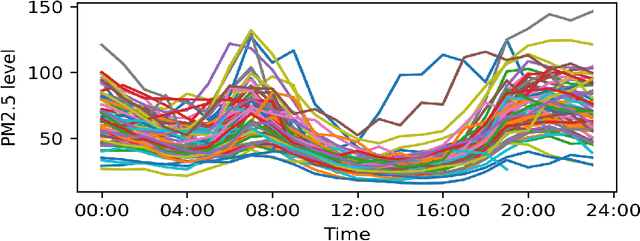
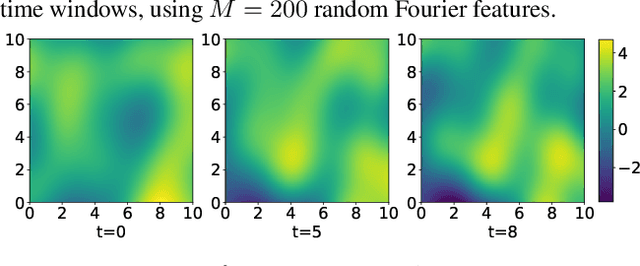
Monitoring air pollution is of vital importance to the overall health of the population. Unfortunately, devices that can measure air quality can be expensive, and many cities in low and middle-income countries have to rely on a sparse allocation of them. In this paper, we investigate the use of Gaussian Processes for both nowcasting the current air-pollution in places where there are no sensors and forecasting the air-pollution in the future at the sensor locations. In particular, we focus on the city of Kampala in Uganda, using data from AirQo's network of sensors. We demonstrate the advantage of removing outliers, compare different kernel functions and additional inputs. We also compare two sparse approximations to allow for the large amounts of temporal data in the dataset.

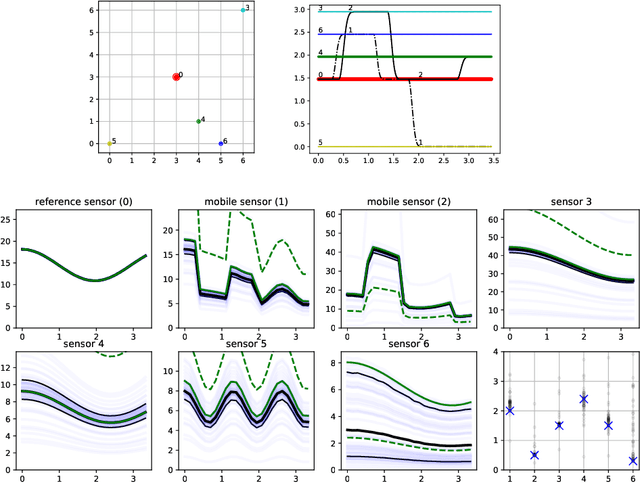
Modelling calibration uncertainty in networks of environmental sensors

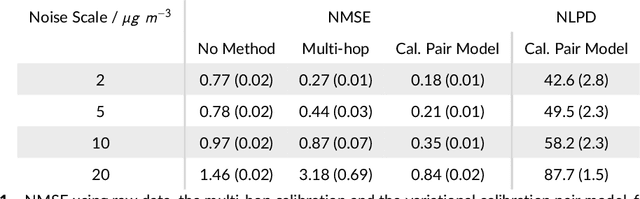
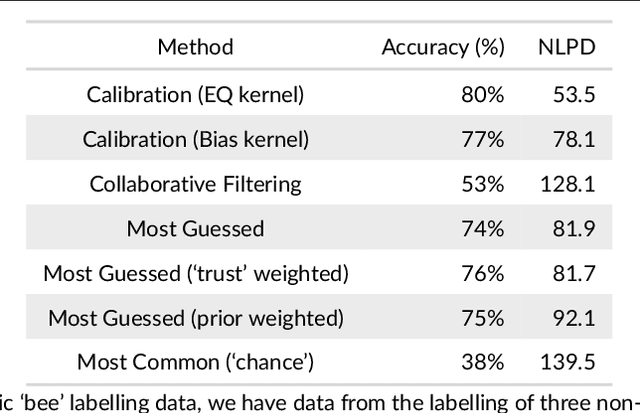
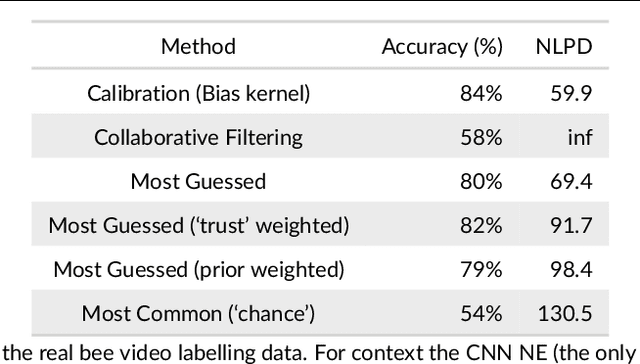
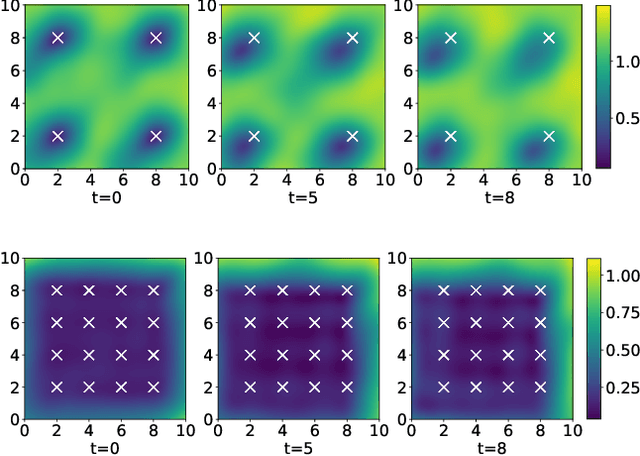
Networks of low-cost sensors are becoming ubiquitous, but often suffer from poor accuracies and drift. Regular colocation with reference sensors allows recalibration but is complicated and expensive. Alternatively the calibration can be transferred using low-cost, mobile sensors. However inferring the calibration (with uncertainty) becomes difficult. We propose a variational approach to model the calibration across the network. We demonstrate the approach on synthetic and real air pollution data, and find it can perform better than the state of the art (multi-hop calibration). We extend it to categorical data produced by citizen-scientist labelling. In Summary: The method achieves uncertainty-quantified calibration, which has been one of the barriers to low-cost sensor deployment and citizen-science research.

Adjoint-aided inference of Gaussian process driven differential equations

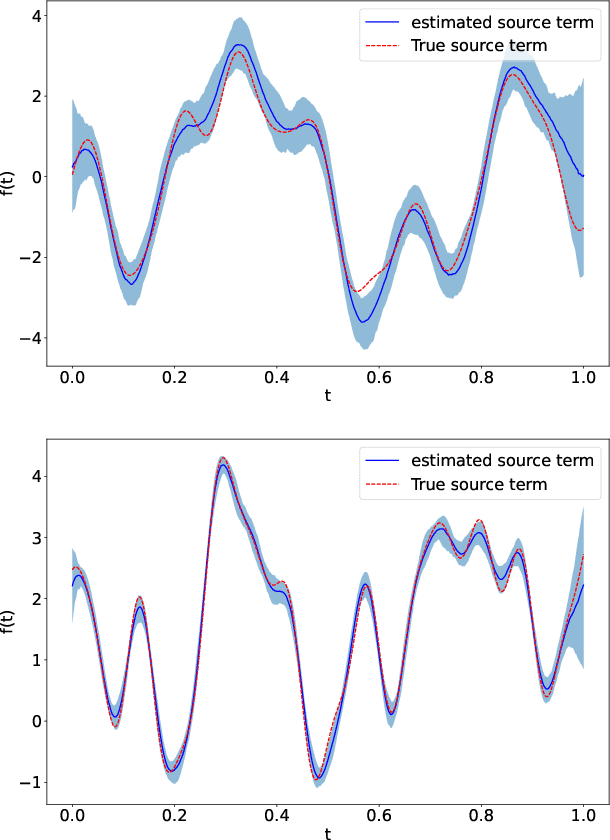
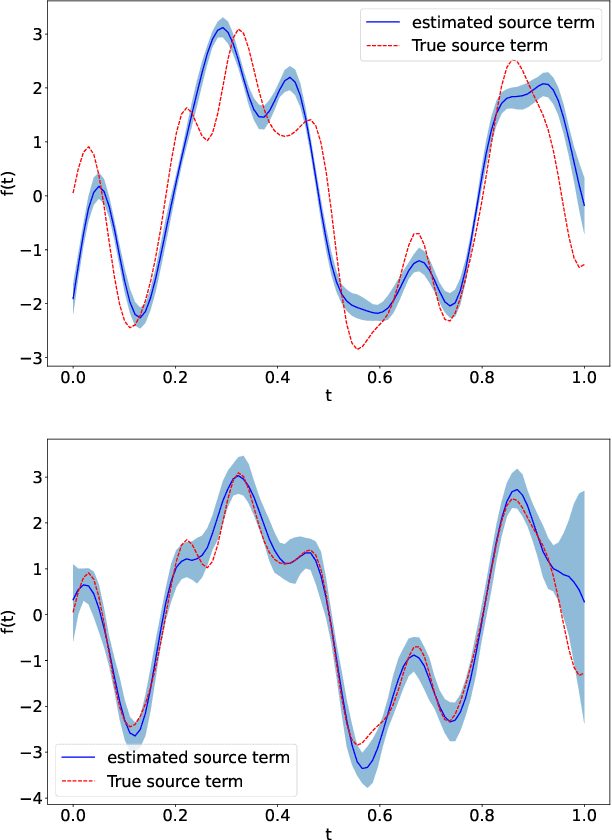
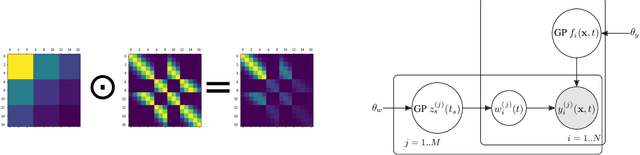
Linear systems occur throughout engineering and the sciences, most notably as differential equations. In many cases the forcing function for the system is unknown, and interest lies in using noisy observations of the system to infer the forcing, as well as other unknown parameters. In differential equations, the forcing function is an unknown function of the independent variables (typically time and space), and can be modelled as a Gaussian process (GP). In this paper we show how the adjoint of a linear system can be used to efficiently infer forcing functions modelled as GPs, after using a truncated basis expansion of the GP kernel. We show how exact conjugate Bayesian inference for the truncated GP can be achieved, in many cases with substantially lower computation than would be required using MCMC methods. We demonstrate the approach on systems of both ordinary and partial differential equations, and by testing on synthetic data, show that the basis expansion approach approximates well the true forcing with a modest number of basis vectors. Finally, we show how to infer point estimates for the non-linear model parameters, such as the kernel length-scales, using Bayesian optimisation.

Machine Learning for a Low-cost Air Pollution Network

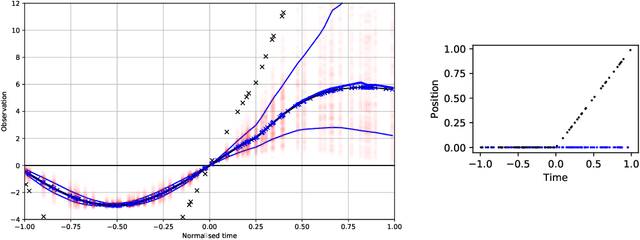
Data collection in economically constrained countries often necessitates using approximate and biased measurements due to the low-cost of the sensors used. This leads to potentially invalid predictions and poor policies or decision making. This is especially an issue if methods from resource-rich regions are applied without handling these additional constraints. In this paper we show, through the use of an air pollution network example, how using probabilistic machine learning can mitigate some of the technical constraints. Specifically we experiment with modelling the calibration for individual sensors as either distributions or Gaussian processes over time, and discuss the wider issues around the decision process.