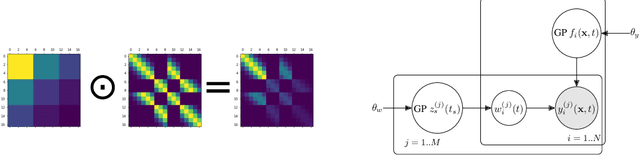
Shallow and Deep Nonparametric Convolutions for Gaussian Processes

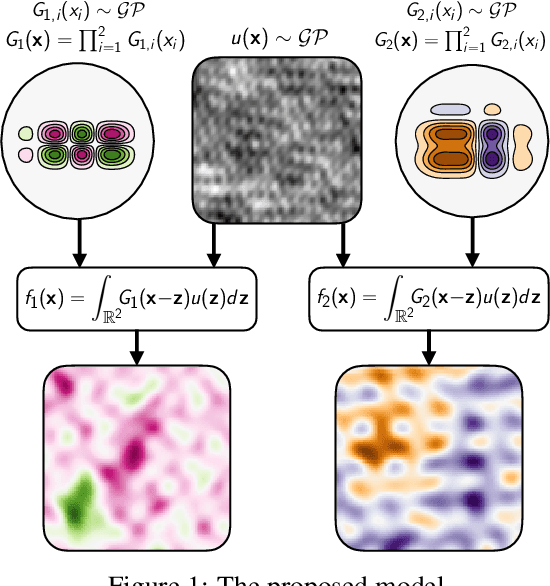
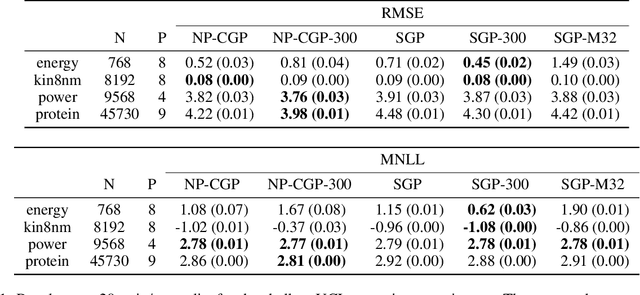
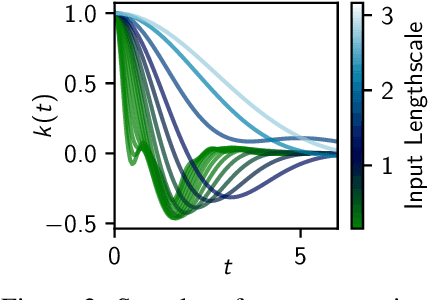
A key challenge in the practical application of Gaussian processes (GPs) is selecting a proper covariance function. The moving average, or process convolutions, construction of GPs allows some additional flexibility, but still requires choosing a proper smoothing kernel, which is non-trivial. Previous approaches have built covariance functions by using GP priors over the smoothing kernel, and by extension the covariance, as a way to bypass the need to specify it in advance. However, such models have been limited in several ways: they are restricted to single dimensional inputs, e.g. time; they only allow modelling of single outputs and they do not scale to large datasets since inference is not straightforward. In this paper, we introduce a nonparametric process convolution formulation for GPs that alleviates these weaknesses by using a functional sampling approach based on Matheron's rule to perform fast sampling using interdomain inducing variables. Furthermore, we propose a composition of these nonparametric convolutions that serves as an alternative to classic deep GP models, and allows the covariance functions of the intermediate layers to be inferred from the data. We test the performance of our model on benchmarks for single output GPs, multiple output GPs and deep GPs and find that in many cases our approach can provide improvements over standard GP models.

Learning Nonparametric Volterra Kernels with Gaussian Processes

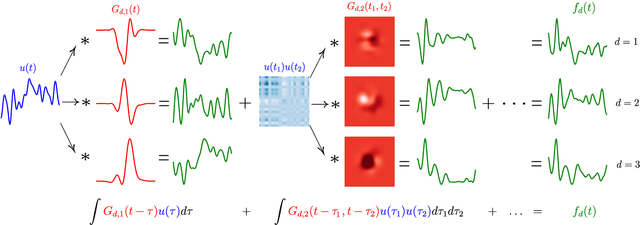
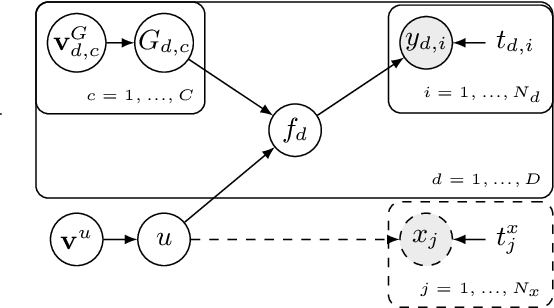
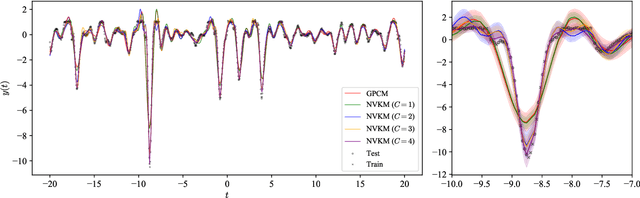
This paper introduces a method for the nonparametric Bayesian learning of nonlinear operators, through the use of the Volterra series with kernels represented using Gaussian processes (GPs), which we term the nonparametric Volterra kernels model (NVKM). When the input function to the operator is unobserved and has a GP prior, the NVKM constitutes a powerful method for both single and multiple output regression, and can be viewed as a nonlinear and nonparametric latent force model. When the input function is observed, the NVKM can be used to perform Bayesian system identification. We use recent advances in efficient sampling of explicit functions from GPs to map process realisations through the Volterra series without resorting to numerical integration, allowing scalability through doubly stochastic variational inference, and avoiding the need for Gaussian approximations of the output processes. We demonstrate the performance of the model for both multiple output regression and system identification using standard benchmarks.

Machine Learning for a Low-cost Air Pollution Network

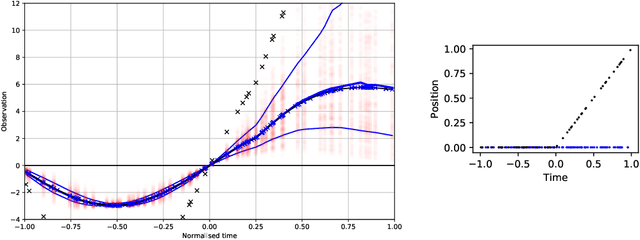
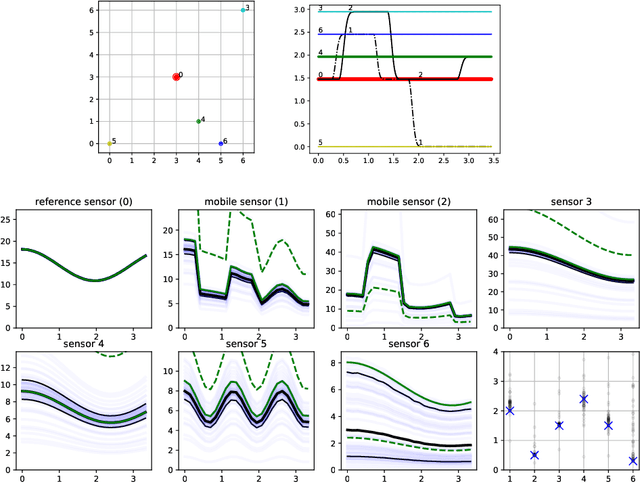
Data collection in economically constrained countries often necessitates using approximate and biased measurements due to the low-cost of the sensors used. This leads to potentially invalid predictions and poor policies or decision making. This is especially an issue if methods from resource-rich regions are applied without handling these additional constraints. In this paper we show, through the use of an air pollution network example, how using probabilistic machine learning can mitigate some of the technical constraints. Specifically we experiment with modelling the calibration for individual sensors as either distributions or Gaussian processes over time, and discuss the wider issues around the decision process.

The Limitations of Model Uncertainty in Adversarial Settings

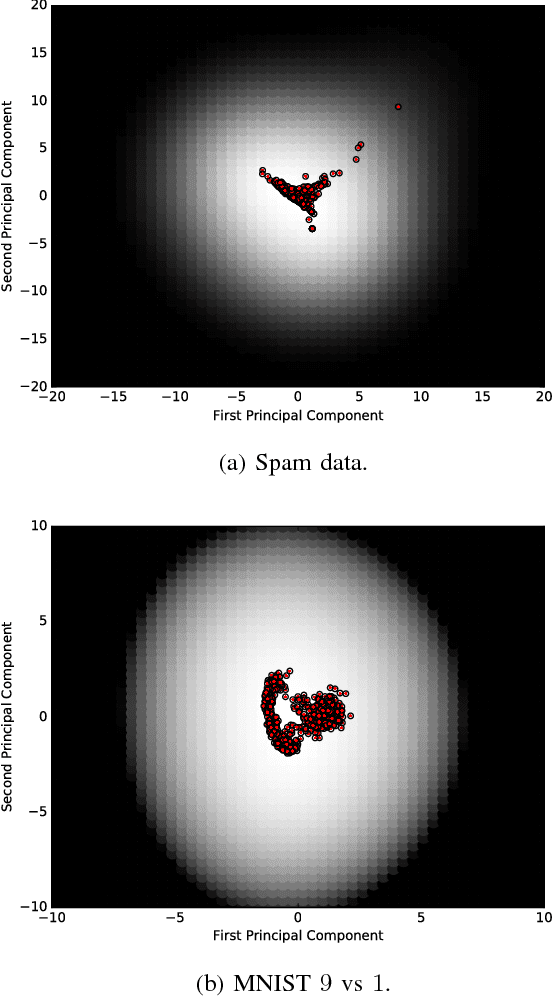
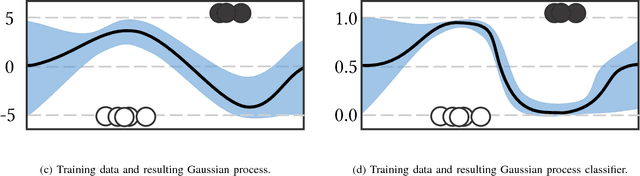
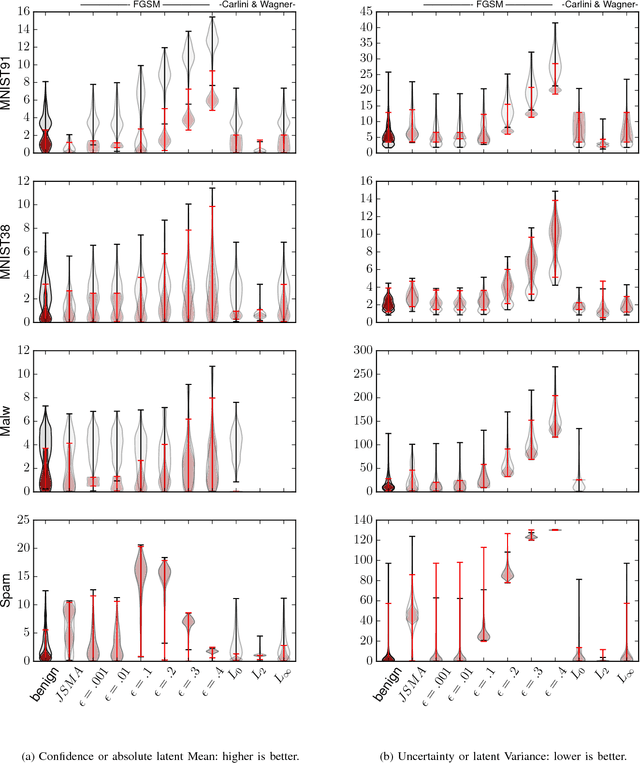
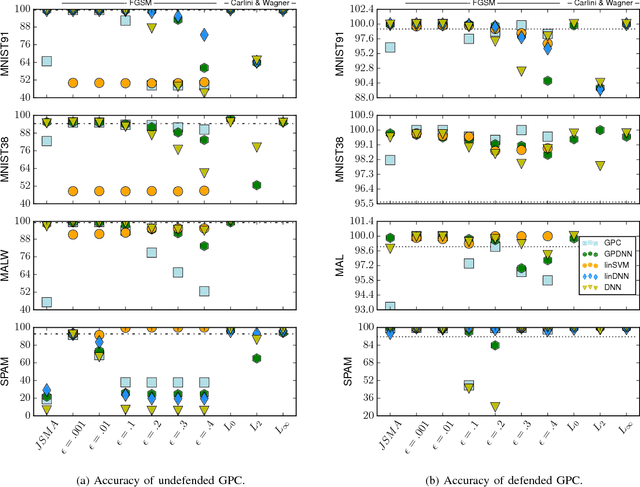
Machine learning models are vulnerable to adversarial examples: minor perturbations to input samples intended to deliberately cause misclassification. Many defenses have led to an arms race-we thus study a promising, recent trend in this setting, Bayesian uncertainty measures. These measures allow a classifier to provide principled confidence and uncertainty for an input, where the latter refers to how usual the input is. We focus on Gaussian processes (GP), a classifier providing such principled uncertainty and confidence measures. Using correctly classified benign data as comparison, GP's intrinsic uncertainty and confidence deviate for misclassified benign samples and misclassified adversarial examples. We therefore introduce high-confidence-low-uncertainty adversarial examples: adversarial examples crafted maximizing GP confidence and minimizing GP uncertainty. Visual inspection shows HCLU adversarial examples are malicious, and resemble the original rather than the target class. HCLU adversarial examples also transfer to other classifiers. We focus on transferability to other algorithms providing uncertainty measures, and find that a Bayesian neural network confidently misclassifies HCLU adversarial examples. We conclude that uncertainty and confidence, even in the Bayesian sense, can be circumvented by both white-box and black-box attackers.

Killing Three Birds with one Gaussian Process: Analyzing Attack Vectors on Classification

The wide usage of Machine Learning (ML) has lead to research on the attack vectors and vulnerability of these systems. The defenses in this area are however still an open problem, and often lead to an arms race. We define a naive, secure classifier at test time and show that a Gaussian Process (GP) is an instance of this classifier given two assumptions: one concerns the distances in the training data, the other rejection at test time. Using these assumptions, we are able to show that a classifier is either secure, or generalizes and thus learns. Our analysis also points towards another factor influencing robustness, the curvature of the classifier. This connection is not unknown for linear models, but GP offer an ideal framework to study this relationship for nonlinear classifiers. We evaluate on five security and two computer vision datasets applying test and training time attacks and membership inference. We show that we only change which attacks are needed to succeed, instead of alleviating the threat. Only for membership inference, there is a setting in which attacks are unsuccessful (<10% increase in accuracy over random guess). Given these results, we define a classification scheme based on voting, ParGP. This allows us to decide how many points vote and how large the agreement on a class has to be. This ensures a classification output only in cases when there is evidence for a decision, where evidence is parametrized. We evaluate this scheme and obtain promising results.