Impatient Bandits: Optimizing Recommendations for the Long-Term Without Delay

Recommender systems are a ubiquitous feature of online platforms. Increasingly, they are explicitly tasked with increasing users' long-term satisfaction. In this context, we study a content exploration task, which we formalize as a multi-armed bandit problem with delayed rewards. We observe that there is an apparent trade-off in choosing the learning signal: Waiting for the full reward to become available might take several weeks, hurting the rate at which learning happens, whereas measuring short-term proxy rewards reflects the actual long-term goal only imperfectly. We address this challenge in two steps. First, we develop a predictive model of delayed rewards that incorporates all information obtained to date. Full observations as well as partial (short or medium-term) outcomes are combined through a Bayesian filter to obtain a probabilistic belief. Second, we devise a bandit algorithm that takes advantage of this new predictive model. The algorithm quickly learns to identify content aligned with long-term success by carefully balancing exploration and exploitation. We apply our approach to a podcast recommendation problem, where we seek to identify shows that users engage with repeatedly over two months. We empirically validate that our approach results in substantially better performance compared to approaches that either optimize for short-term proxies, or wait for the long-term outcome to be fully realized.

One-shot Feature-Preserving Point Cloud Simplification with Gaussian Processes on Riemannian Manifolds

The processing, storage and transmission of large-scale point clouds is an ongoing challenge in the computer vision community which hinders progress in the application of 3D models to real-world settings, such as autonomous driving, virtual reality and remote sensing. We propose a novel, one-shot point cloud simplification method which preserves both the salient structural features and the overall shape of a point cloud without any prior surface reconstruction step. Our method employs Gaussian processes with kernels defined on Riemannian manifolds, allowing us to model the surface variation function across any given point cloud. A simplified version of the original cloud is obtained by sequentially selecting points using a greedy sparsification scheme. The selection criterion used for this scheme ensures that the simplified cloud best represents the surface variation of the original point cloud. We evaluate our method on several benchmark datasets, compare it to a range of existing methods and show that our method is competitive both in terms of empirical performance and computational efficiency.

Shallow and Deep Nonparametric Convolutions for Gaussian Processes

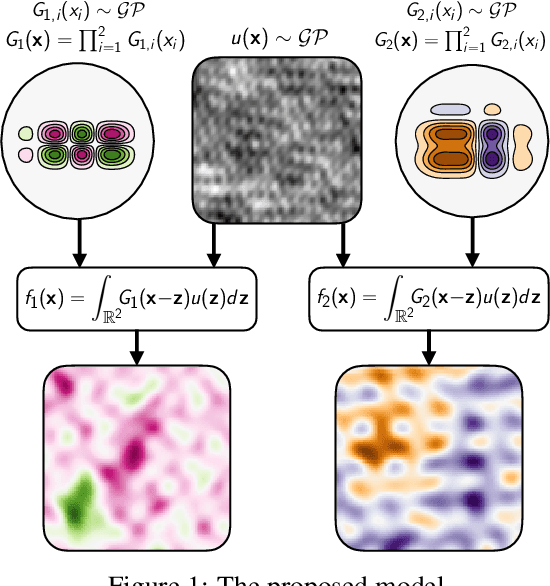
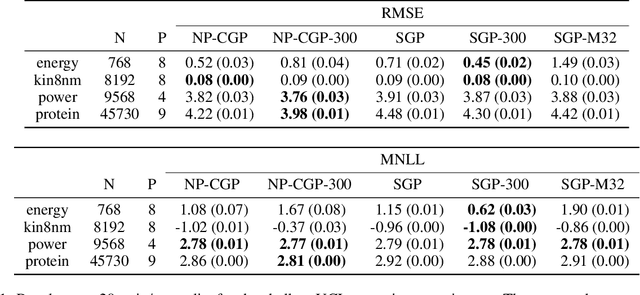
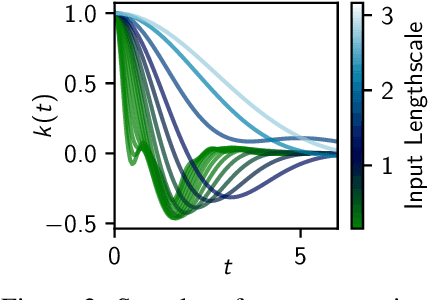
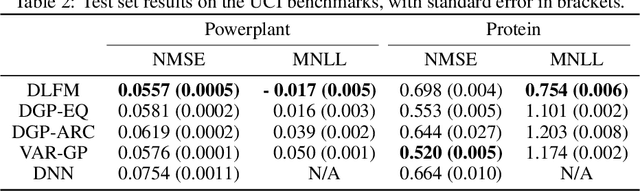
A key challenge in the practical application of Gaussian processes (GPs) is selecting a proper covariance function. The moving average, or process convolutions, construction of GPs allows some additional flexibility, but still requires choosing a proper smoothing kernel, which is non-trivial. Previous approaches have built covariance functions by using GP priors over the smoothing kernel, and by extension the covariance, as a way to bypass the need to specify it in advance. However, such models have been limited in several ways: they are restricted to single dimensional inputs, e.g. time; they only allow modelling of single outputs and they do not scale to large datasets since inference is not straightforward. In this paper, we introduce a nonparametric process convolution formulation for GPs that alleviates these weaknesses by using a functional sampling approach based on Matheron's rule to perform fast sampling using interdomain inducing variables. Furthermore, we propose a composition of these nonparametric convolutions that serves as an alternative to classic deep GP models, and allows the covariance functions of the intermediate layers to be inferred from the data. We test the performance of our model on benchmarks for single output GPs, multiple output GPs and deep GPs and find that in many cases our approach can provide improvements over standard GP models.

Compositional Modeling of Nonlinear Dynamical Systems with ODE-based Random Features

Effectively modeling phenomena present in highly nonlinear dynamical systems whilst also accurately quantifying uncertainty is a challenging task, which often requires problem-specific techniques. We present a novel, domain-agnostic approach to tackling this problem, using compositions of physics-informed random features, derived from ordinary differential equations. The architecture of our model leverages recent advances in approximate inference for deep Gaussian processes, such as layer-wise weight-space approximations which allow us to incorporate random Fourier features, and stochastic variational inference for approximate Bayesian inference. We provide evidence that our model is capable of capturing highly nonlinear behaviour in real-world multivariate time series data. In addition, we find that our approach achieves comparable performance to a number of other probabilistic models on benchmark regression tasks.