Scalable Multi-Output Gaussian Processes with Stochastic Variational Inference

The Multi-Output Gaussian Process is is a popular tool for modelling data from multiple sources. A typical choice to build a covariance function for a MOGP is the Linear Model of Coregionalization (LMC) which parametrically models the covariance between outputs. The Latent Variable MOGP (LV-MOGP) generalises this idea by modelling the covariance between outputs using a kernel applied to latent variables, one per output, leading to a flexible MOGP model that allows efficient generalization to new outputs with few data points. Computational complexity in LV-MOGP grows linearly with the number of outputs, which makes it unsuitable for problems with a large number of outputs. In this paper, we propose a stochastic variational inference approach for the LV-MOGP that allows mini-batches for both inputs and outputs, making computational complexity per training iteration independent of the number of outputs.

Longitudinal prediction of DNA methylation to forecast epigenetic outcomes

Interrogating the evolution of biological changes at early stages of life requires longitudinal profiling of molecules, such as DNA methylation, which can be challenging with children. We introduce a probabilistic and longitudinal machine learning framework based on multi-mean Gaussian processes (GPs), accounting for individual and gene correlations across time. This method provides future predictions of DNA methylation status at different individual ages while accounting for uncertainty. Our model is trained on a birth cohort of children with methylation profiled at ages 0-4, and we demonstrated that the status of methylation sites for each child can be accurately predicted at ages 5-7. We show that methylation profiles predicted by multi-mean GPs can be used to estimate other phenotypes, such as epigenetic age, and enable comparison to other health measures of interest. This approach encourages epigenetic studies to move towards longitudinal design for investigating epigenetic changes during development, ageing and disease progression.

Machine Learning for a Low-cost Air Pollution Network

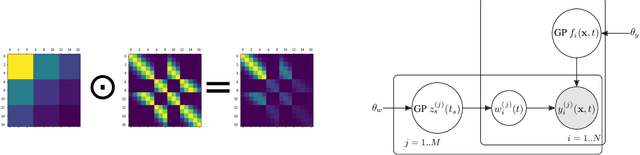
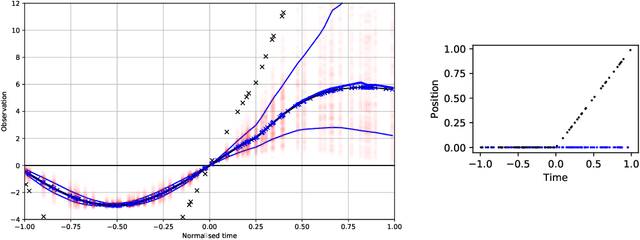
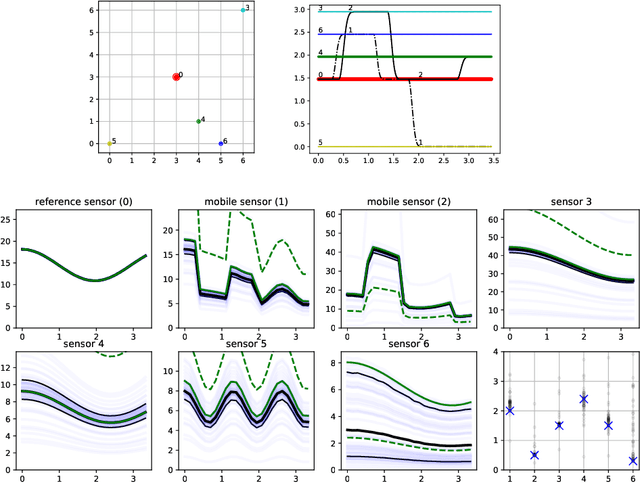
Data collection in economically constrained countries often necessitates using approximate and biased measurements due to the low-cost of the sensors used. This leads to potentially invalid predictions and poor policies or decision making. This is especially an issue if methods from resource-rich regions are applied without handling these additional constraints. In this paper we show, through the use of an air pollution network example, how using probabilistic machine learning can mitigate some of the technical constraints. Specifically we experiment with modelling the calibration for individual sensors as either distributions or Gaussian processes over time, and discuss the wider issues around the decision process.

Differentially Private Regression and Classification with Sparse Gaussian Processes

A continuing challenge for machine learning is providing methods to perform computation on data while ensuring the data remains private. In this paper we build on the provable privacy guarantees of differential privacy which has been combined with Gaussian processes through the previously published \emph{cloaking method}. In this paper we solve several shortcomings of this method, starting with the problem of predictions in regions with low data density. We experiment with the use of inducing points to provide a sparse approximation and show that these can provide robust differential privacy in outlier areas and at higher dimensions. We then look at classification, and modify the Laplace approximation approach to provide differentially private predictions. We then combine this with the sparse approximation and demonstrate the capability to perform classification in high dimensions. We finally explore the issue of hyperparameter selection and develop a method for their private selection. This paper and associated libraries provide a robust toolkit for combining differential privacy and GPs in a practical manner.

Physically-inspired Gaussian processes for transcriptional regulation in Drosophila melanogaster

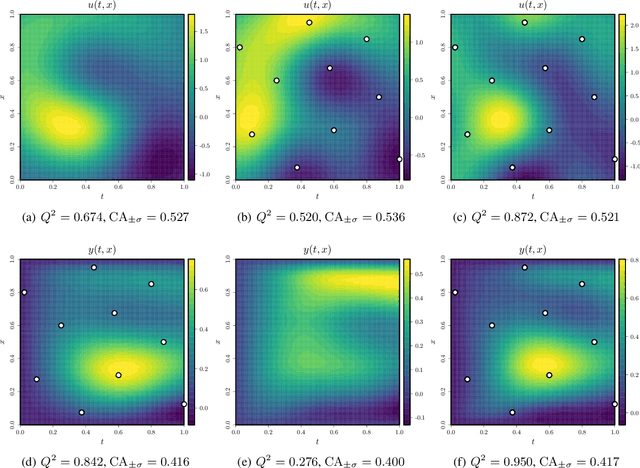
The regulatory process in Drosophila melanogaster is thoroughly studied for understanding several principles in systems biology. Since transcriptional regulation of the Drosophila depends on spatiotemporal interactions between mRNA expressions and gap-gene proteins, proper physically-inspired stochastic models are required to describe the existing link between both biological quantities. Many studies have shown that the use of Gaussian processes (GPs) and differential equations yields promising inference results when modelling regulatory processes. In order to exploit the benefits of GPs, two types of physically-inspired GPs based on the reaction-diffusion equation are further investigated in this paper. The main difference between both approaches lies on whether the GP prior is placed: either over mRNA expressions or protein concentrations. Contrarily to other stochastic frameworks, discretising the spatial space is not required here. Both GP models are tested under different conditions depending on the availability of biological data. Finally, their performances are assessed using a high-resolution dataset describing the blastoderm stage of the early embryo of Drosophila.

A Tucker decomposition process for probabilistic modeling of diffusion magnetic resonance imaging

Diffusion magnetic resonance imaging (dMRI) is an emerging medical technique used for describing water diffusion in an organic tissue. Typically, rank-2 tensors quantify this diffusion. From this quantification, it is possible to calculate relevant scalar measures (i.e. fractional anisotropy and mean diffusivity) employed in clinical diagnosis of neurological diseases. Nonetheless, 2nd-order tensors fail to represent complex tissue structures like crossing fibers. To overcome this limitation, several researchers proposed a diffusion representation with higher order tensors (HOT), specifically 4th and 6th orders. However, the current acquisition protocols of dMRI data allow images with a spatial resolution between 1 $mm^3$ and 2 $mm^3$. This voxel size is much smaller than tissue structures. Therefore, several clinical procedures derived from dMRI may be inaccurate. Interpolation has been used to enhance resolution of dMRI in a tensorial space. Most interpolation methods are valid only for rank-2 tensors and a generalization for HOT data is missing. In this work, we propose a novel stochastic process called Tucker decomposition process (TDP) for performing HOT data interpolation. Our model is based on the Tucker decomposition and Gaussian processes as parameters of the TDP. We test the TDP in 2nd, 4th and 6th rank HOT fields. For rank-2 tensors, we compare against direct interpolation, log-Euclidean approach and Generalized Wishart processes. For rank-4 and rank-6 tensors we compare against direct interpolation. Results obtained show that TDP interpolates accurately the HOT fields and generalizes to any rank.

Generalized Wishart processes for interpolation over diffusion tensor fields

Diffusion Magnetic Resonance Imaging (dMRI) is a non-invasive tool for watching the microstructure of fibrous nerve and muscle tissue. From dMRI, it is possible to estimate 2-rank diffusion tensors imaging (DTI) fields, that are widely used in clinical applications: tissue segmentation, fiber tractography, brain atlas construction, brain conductivity models, among others. Due to hardware limitations of MRI scanners, DTI has the difficult compromise between spatial resolution and signal noise ratio (SNR) during acquisition. For this reason, the data are often acquired with very low resolution. To enhance DTI data resolution, interpolation provides an interesting software solution. The aim of this work is to develop a methodology for DTI interpolation that enhance the spatial resolution of DTI fields. We assume that a DTI field follows a recently introduced stochastic process known as a generalized Wishart process (GWP), which we use as a prior over the diffusion tensor field. For posterior inference, we use Markov Chain Monte Carlo methods. We perform experiments in toy and real data. Results of GWP outperform other methods in the literature, when compared in different validation protocols.

Kernels for Vector-Valued Functions: a Review

Kernel methods are among the most popular techniques in machine learning. From a frequentist/discriminative perspective they play a central role in regularization theory as they provide a natural choice for the hypotheses space and the regularization functional through the notion of reproducing kernel Hilbert spaces. From a Bayesian/generative perspective they are the key in the context of Gaussian processes, where the kernel function is also known as the covariance function. Traditionally, kernel methods have been used in supervised learning problem with scalar outputs and indeed there has been a considerable amount of work devoted to designing and learning kernels. More recently there has been an increasing interest in methods that deal with multiple outputs, motivated partly by frameworks like multitask learning. In this paper, we review different methods to design or learn valid kernel functions for multiple outputs, paying particular attention to the connection between probabilistic and functional methods.