Longitudinal prediction of DNA methylation to forecast epigenetic outcomes

Interrogating the evolution of biological changes at early stages of life requires longitudinal profiling of molecules, such as DNA methylation, which can be challenging with children. We introduce a probabilistic and longitudinal machine learning framework based on multi-mean Gaussian processes (GPs), accounting for individual and gene correlations across time. This method provides future predictions of DNA methylation status at different individual ages while accounting for uncertainty. Our model is trained on a birth cohort of children with methylation profiled at ages 0-4, and we demonstrated that the status of methylation sites for each child can be accurately predicted at ages 5-7. We show that methylation profiles predicted by multi-mean GPs can be used to estimate other phenotypes, such as epigenetic age, and enable comparison to other health measures of interest. This approach encourages epigenetic studies to move towards longitudinal design for investigating epigenetic changes during development, ageing and disease progression.

Personalized Longitudinal Assessment of Multiple Sclerosis Using Smartphones

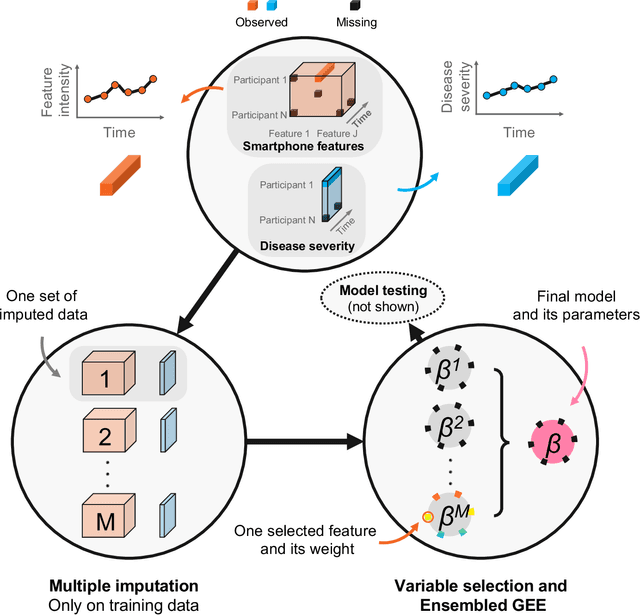
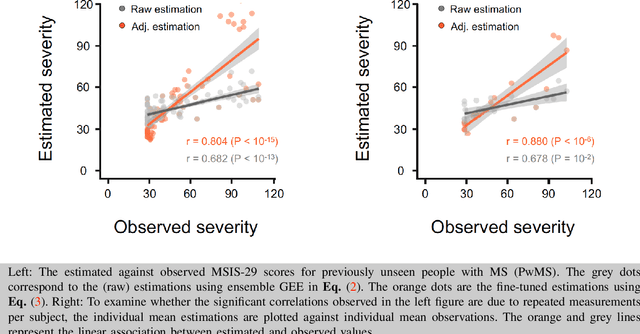
Personalized longitudinal disease assessment is central to quickly diagnosing, appropriately managing, and optimally adapting the therapeutic strategy of multiple sclerosis (MS). It is also important for identifying the idiosyncratic subject-specific disease profiles. Here, we design a novel longitudinal model to map individual disease trajectories in an automated way using sensor data that may contain missing values. First, we collect digital measurements related to gait and balance, and upper extremity functions using sensor-based assessments administered on a smartphone. Next, we treat missing data via imputation. We then discover potential markers of MS by employing a generalized estimation equation. Subsequently, parameters learned from multiple training datasets are ensembled to form a simple, unified longitudinal predictive model to forecast MS over time in previously unseen people with MS. To mitigate potential underestimation for individuals with severe disease scores, the final model incorporates additional subject-specific fine-tuning using data from the first day. The results show that the proposed model is promising to achieve personalized longitudinal MS assessment; they also suggest that features related to gait and balance as well as upper extremity function, remotely collected from sensor-based assessments, may be useful digital markers for predicting MS over time.

Model-based clustering in very high dimensions via adaptive projections

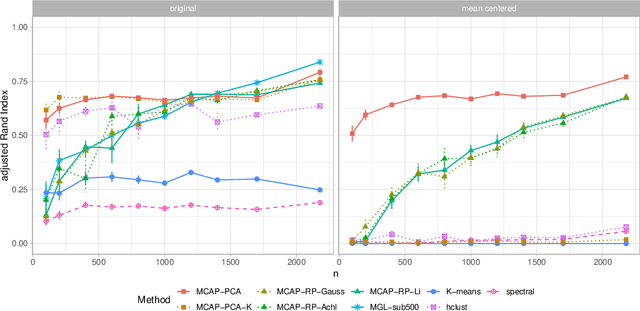
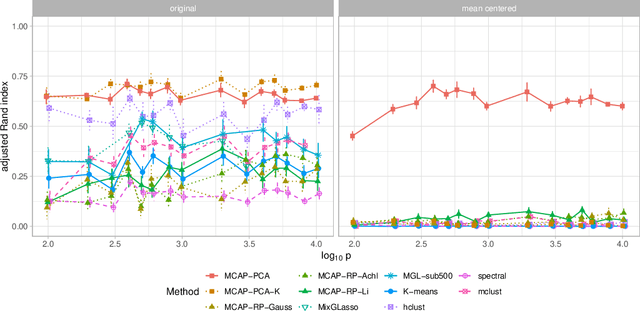
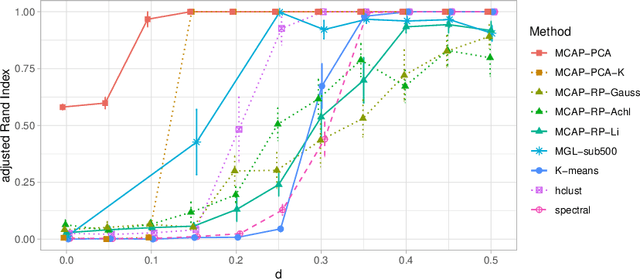
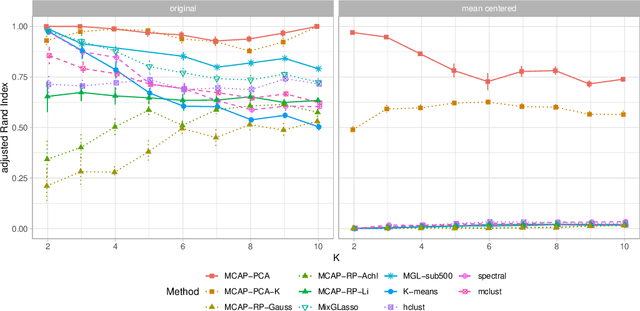
Mixture models are a standard approach to dealing with heterogeneous data with non-i.i.d. structure. However, when the dimension $p$ is large relative to sample size $n$ and where either or both of means and covariances/graphical models may differ between the latent groups, mixture models face statistical and computational difficulties and currently available methods cannot realistically go beyond $p \! \sim \! 10^4$ or so. We propose an approach called Model-based Clustering via Adaptive Projections (MCAP). Instead of estimating mixtures in the original space, we work with a low-dimensional representation obtained by linear projection. The projection dimension itself plays an important role and governs a type of bias-variance tradeoff with respect to recovery of the relevant signals. MCAP sets the projection dimension automatically in a data-adaptive manner, using a proxy for the assignment risk. Combining a full covariance formulation with the adaptive projection allows detection of both mean and covariance signals in very high dimensional problems. We show real-data examples in which covariance signals are reliably detected in problems with $p \! \sim \! 10^4$ or more, and simulations going up to $p = 10^6$. In some examples, MCAP performs well even when the mean signal is entirely removed, leaving differential covariance structure in the high-dimensional space as the only signal. Across a number of regimes, MCAP performs as well or better than a range of existing methods, including a recently-proposed $\ell_1$-penalized approach; and performance remains broadly stable with increasing dimension. MCAP can be run "out of the box" and is fast enough for interactive use on large-$p$ problems using standard desktop computing resources.

High-dimensional regression over disease subgroups

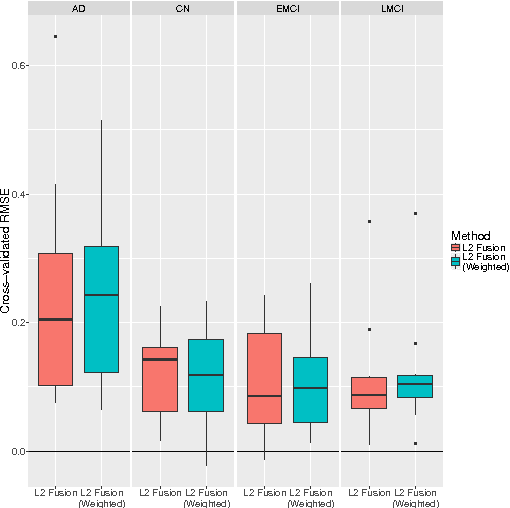
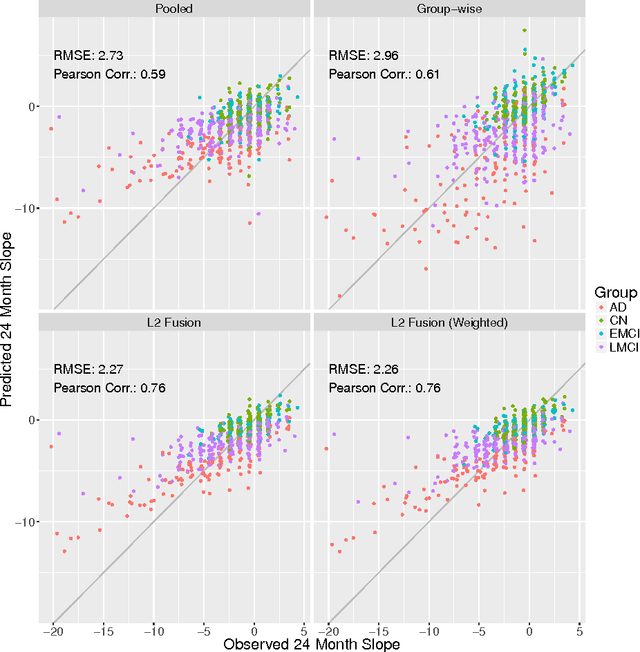
We consider high-dimensional regression over subgroups of observations. Our work is motivated by biomedical problems, where disease subtypes, for example, may differ with respect to underlying regression models, but sample sizes at the subgroup-level may be limited. We focus on the case in which subgroup-specific models may be expected to be similar but not necessarily identical. Our approach is to treat subgroups as related problem instances and jointly estimate subgroup-specific regression coefficients. This is done in a penalized framework, combining an $\ell_1$ term with an additional term that penalizes differences between subgroup-specific coefficients. This gives solutions that are globally sparse but that allow information-sharing between the subgroups. We present algorithms for estimation and empirical results on simulated data and using Alzheimer's disease, amyotrophic lateral sclerosis and cancer datasets. These examples demonstrate the gains our approach can offer in terms of prediction and the ability to estimate subgroup-specific sparsity patterns.