Longitudinal prediction of DNA methylation to forecast epigenetic outcomes

Interrogating the evolution of biological changes at early stages of life requires longitudinal profiling of molecules, such as DNA methylation, which can be challenging with children. We introduce a probabilistic and longitudinal machine learning framework based on multi-mean Gaussian processes (GPs), accounting for individual and gene correlations across time. This method provides future predictions of DNA methylation status at different individual ages while accounting for uncertainty. Our model is trained on a birth cohort of children with methylation profiled at ages 0-4, and we demonstrated that the status of methylation sites for each child can be accurately predicted at ages 5-7. We show that methylation profiles predicted by multi-mean GPs can be used to estimate other phenotypes, such as epigenetic age, and enable comparison to other health measures of interest. This approach encourages epigenetic studies to move towards longitudinal design for investigating epigenetic changes during development, ageing and disease progression.

Latent Variable Multi-output Gaussian Processes for Hierarchical Datasets

Multi-output Gaussian processes (MOGPs) have been introduced to deal with multiple tasks by exploiting the correlations between different outputs. Generally, MOGPs models assume a flat correlation structure between the outputs. However, such a formulation does not account for more elaborate relationships, for instance, if several replicates were observed for each output (which is a typical setting in biological experiments). This paper proposes an extension of MOGPs for hierarchical datasets (i.e. datasets for which the relationships between observations can be represented within a tree structure). Our model defines a tailored kernel function accounting for hierarchical structures in the data to capture different levels of correlations while leveraging the introduction of latent variables to express the underlying dependencies between outputs through a dedicated kernel. This latter feature is expected to significantly improve scalability as the number of tasks increases. An extensive experimental study involving both synthetic and real-world data from genomics and motion capture is proposed to support our claims.

Cluster-Specific Predictions with Multi-Task Gaussian Processes

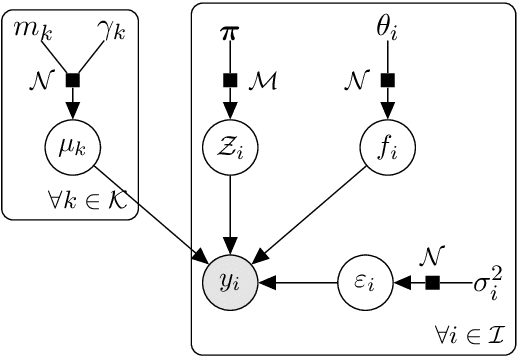
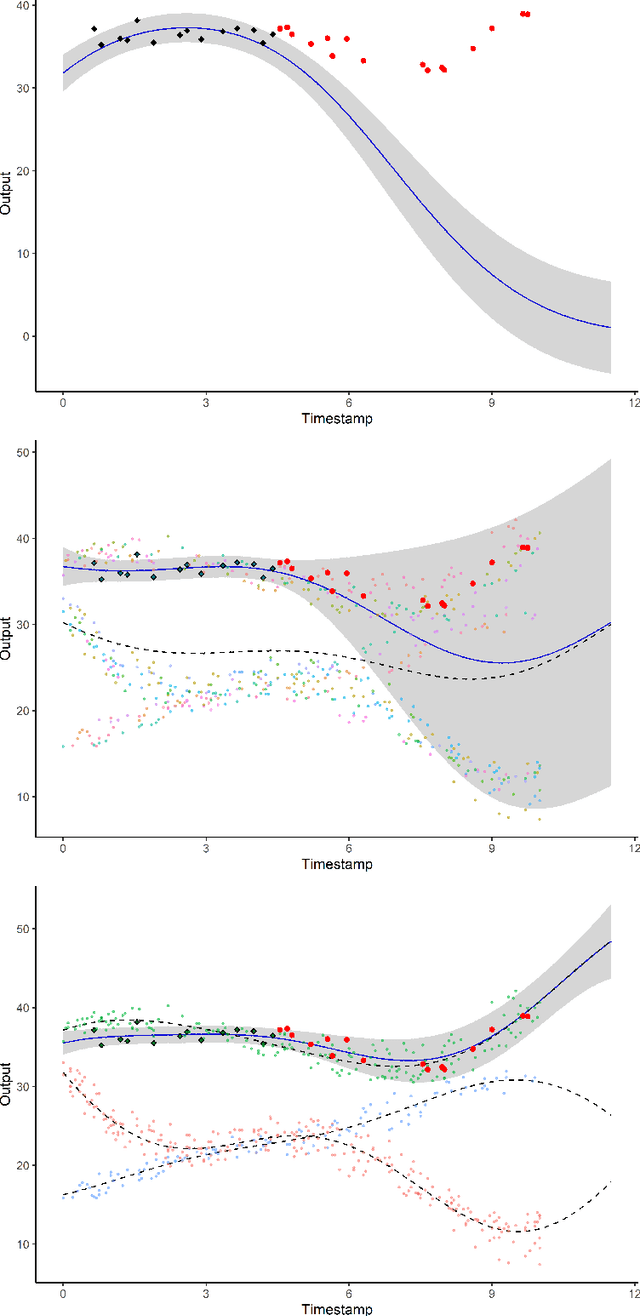
A model involving Gaussian processes (GPs) is introduced to simultaneously handle multi-task learning, clustering, and prediction for multiple functional data. This procedure acts as a model-based clustering method for functional data as well as a learning step for subsequent predictions for new tasks. The model is instantiated as a mixture of multi-task GPs with common mean processes. A variational EM algorithm is derived for dealing with the optimisation of the hyper-parameters along with the hyper-posteriors' estimation of latent variables and processes. We establish explicit formulas for integrating the mean processes and the latent clustering variables within a predictive distribution, accounting for uncertainty on both aspects. This distribution is defined as a mixture of cluster-specific GP predictions, which enhances the performances when dealing with group-structured data. The model handles irregular grid of observations and offers different hypotheses on the covariance structure for sharing additional information across tasks. The performances on both clustering and prediction tasks are assessed through various simulated scenarios and real datasets. The overall algorithm, called MagmaClust, is publicly available as an R package.

MAGMA: Inference and Prediction with Multi-Task Gaussian Processes

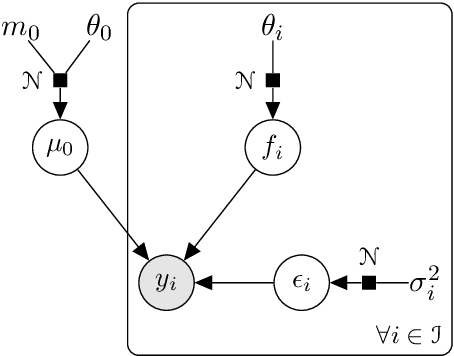
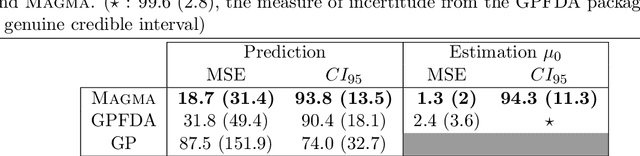
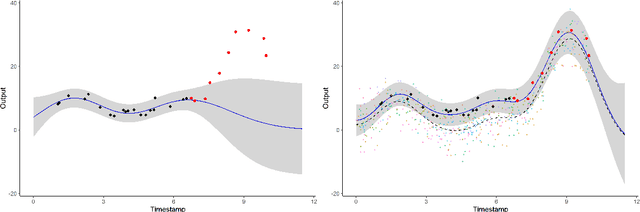
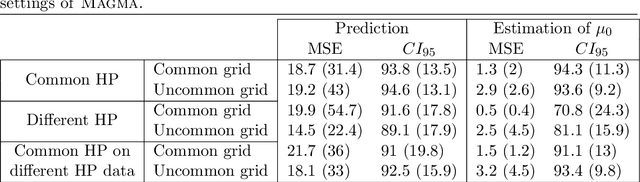
We investigate the problem of multiple time series forecasting, with the objective to improve multiple-step-ahead predictions. We propose a multi-task Gaussian process framework to simultaneously model batches of individuals with a common mean function and a specific covariance structure. This common mean is defined as a Gaussian process for which the hyper-posterior distribution is tractable. Therefore an EM algorithm can be derived for simultaneous hyper-parameters optimisation and hyper-posterior computation. Unlike previous approaches in the literature, we account for uncertainty and handle uncommon grids of observations while maintaining explicit formulations, by modelling the mean process in a non-parametric probabilistic framework. We also provide predictive formulas integrating this common mean process. This approach greatly improves the predictive performance far from observations, where information shared across individuals provides a relevant prior mean. Our overall algorithm is called \textsc{Magma} (standing for Multi tAsk Gaussian processes with common MeAn), and publicly available as a R package. The quality of the mean process estimation, predictive performances, and comparisons to alternatives are assessed in various simulated scenarios and on real datasets.