Cluster-Specific Predictions with Multi-Task Gaussian Processes

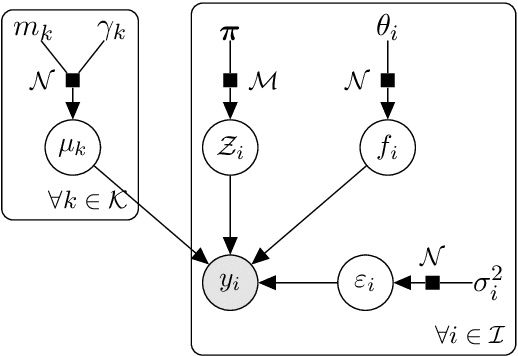
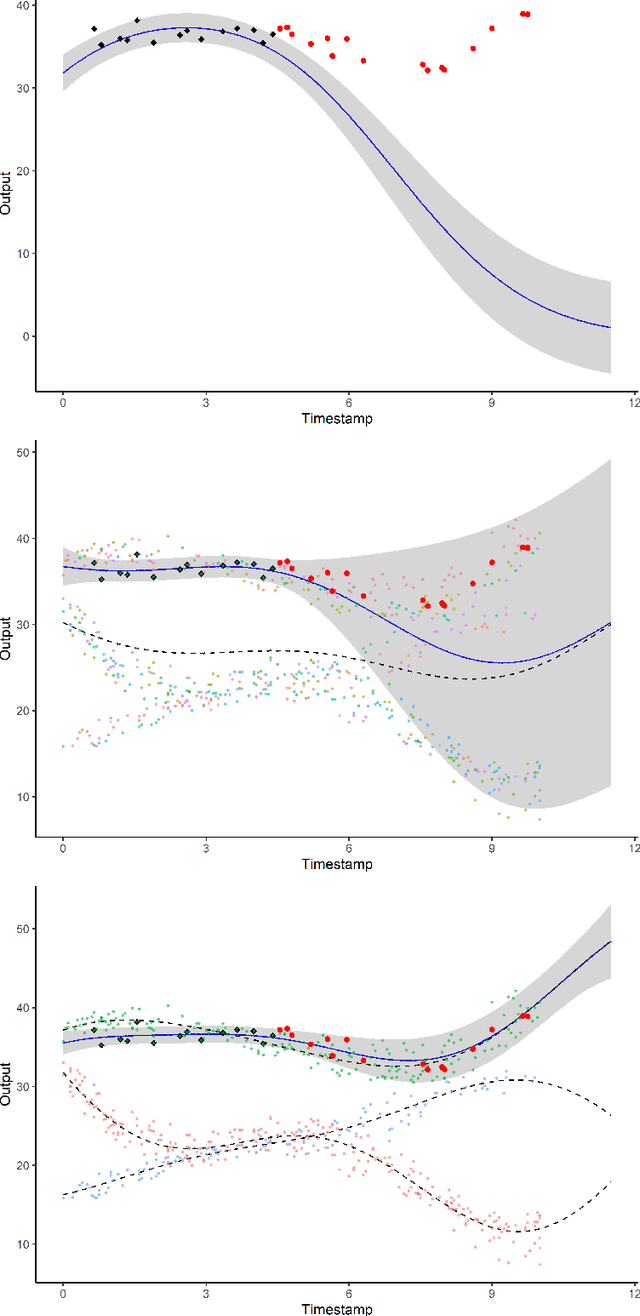
A model involving Gaussian processes (GPs) is introduced to simultaneously handle multi-task learning, clustering, and prediction for multiple functional data. This procedure acts as a model-based clustering method for functional data as well as a learning step for subsequent predictions for new tasks. The model is instantiated as a mixture of multi-task GPs with common mean processes. A variational EM algorithm is derived for dealing with the optimisation of the hyper-parameters along with the hyper-posteriors' estimation of latent variables and processes. We establish explicit formulas for integrating the mean processes and the latent clustering variables within a predictive distribution, accounting for uncertainty on both aspects. This distribution is defined as a mixture of cluster-specific GP predictions, which enhances the performances when dealing with group-structured data. The model handles irregular grid of observations and offers different hypotheses on the covariance structure for sharing additional information across tasks. The performances on both clustering and prediction tasks are assessed through various simulated scenarios and real datasets. The overall algorithm, called MagmaClust, is publicly available as an R package.

MAGMA: Inference and Prediction with Multi-Task Gaussian Processes

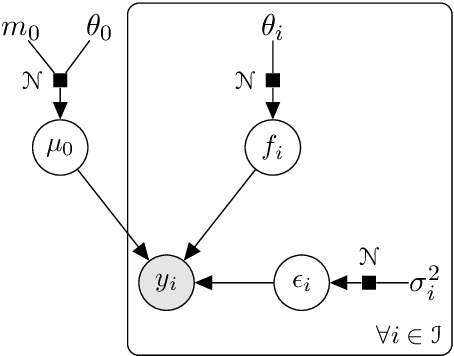
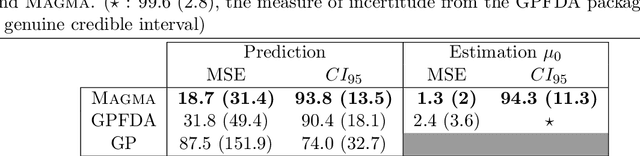
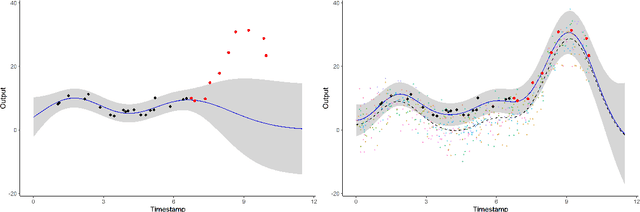
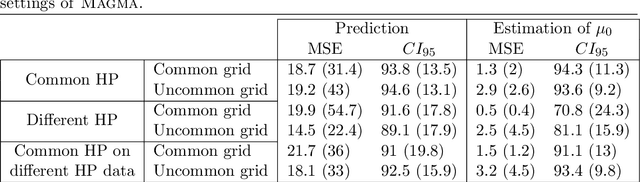
We investigate the problem of multiple time series forecasting, with the objective to improve multiple-step-ahead predictions. We propose a multi-task Gaussian process framework to simultaneously model batches of individuals with a common mean function and a specific covariance structure. This common mean is defined as a Gaussian process for which the hyper-posterior distribution is tractable. Therefore an EM algorithm can be derived for simultaneous hyper-parameters optimisation and hyper-posterior computation. Unlike previous approaches in the literature, we account for uncertainty and handle uncommon grids of observations while maintaining explicit formulations, by modelling the mean process in a non-parametric probabilistic framework. We also provide predictive formulas integrating this common mean process. This approach greatly improves the predictive performance far from observations, where information shared across individuals provides a relevant prior mean. Our overall algorithm is called \textsc{Magma} (standing for Multi tAsk Gaussian processes with common MeAn), and publicly available as a R package. The quality of the mean process estimation, predictive performances, and comparisons to alternatives are assessed in various simulated scenarios and on real datasets.

Risk Bounds for CART Classifiers under a Margin Condition

Risk bounds for Classification and Regression Trees (CART, Breiman et. al. 1984) classifiers are obtained under a margin condition in the binary supervised classification framework. These risk bounds are obtained conditionally on the construction of the maximal deep binary tree and permit to prove that the linear penalty used in the CART pruning algorithm is valid under a margin condition. It is also shown that, conditionally on the construction of the maximal tree, the final selection by test sample does not alter dramatically the estimation accuracy of the Bayes classifier. In the two-class classification framework, the risk bounds that are proved, obtained by using penalized model selection, validate the CART algorithm which is used in many data mining applications such as Biology, Medicine or Image Coding.