Mauricio Alvarez
Latent Variable Multi-output Gaussian Processes for Hierarchical Datasets
Aug 31, 2023Abstract:Multi-output Gaussian processes (MOGPs) have been introduced to deal with multiple tasks by exploiting the correlations between different outputs. Generally, MOGPs models assume a flat correlation structure between the outputs. However, such a formulation does not account for more elaborate relationships, for instance, if several replicates were observed for each output (which is a typical setting in biological experiments). This paper proposes an extension of MOGPs for hierarchical datasets (i.e. datasets for which the relationships between observations can be represented within a tree structure). Our model defines a tailored kernel function accounting for hierarchical structures in the data to capture different levels of correlations while leveraging the introduction of latent variables to express the underlying dependencies between outputs through a dedicated kernel. This latter feature is expected to significantly improve scalability as the number of tasks increases. An extensive experimental study involving both synthetic and real-world data from genomics and motion capture is proposed to support our claims.
Modelling calibration uncertainty in networks of environmental sensors
May 09, 2022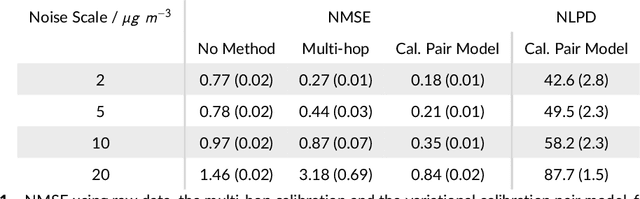

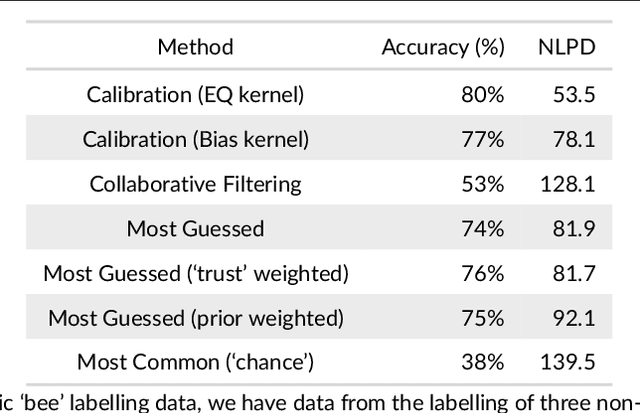
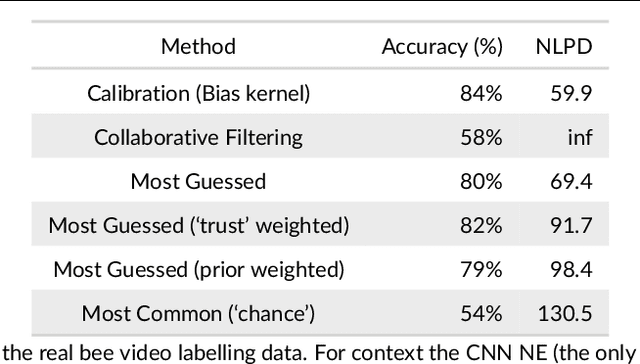
Abstract:Networks of low-cost sensors are becoming ubiquitous, but often suffer from poor accuracies and drift. Regular colocation with reference sensors allows recalibration but is complicated and expensive. Alternatively the calibration can be transferred using low-cost, mobile sensors. However inferring the calibration (with uncertainty) becomes difficult. We propose a variational approach to model the calibration across the network. We demonstrate the approach on synthetic and real air pollution data, and find it can perform better than the state of the art (multi-hop calibration). We extend it to categorical data produced by citizen-scientist labelling. In Summary: The method achieves uncertainty-quantified calibration, which has been one of the barriers to low-cost sensor deployment and citizen-science research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge