Modelling calibration uncertainty in networks of environmental sensors

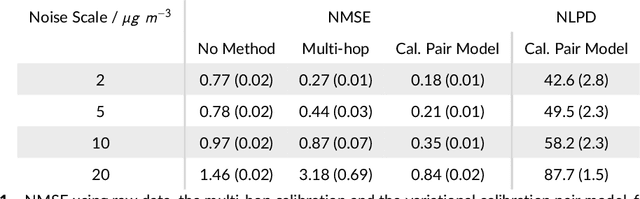
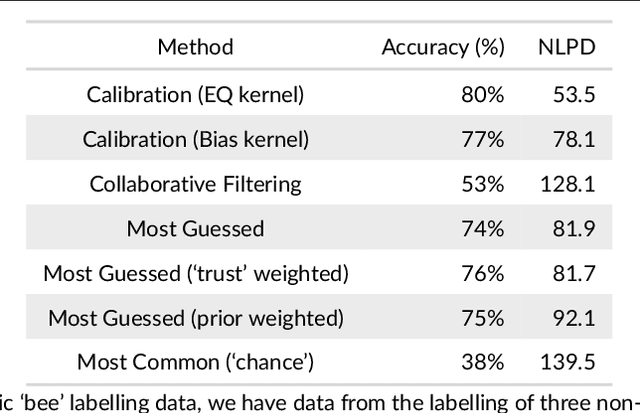
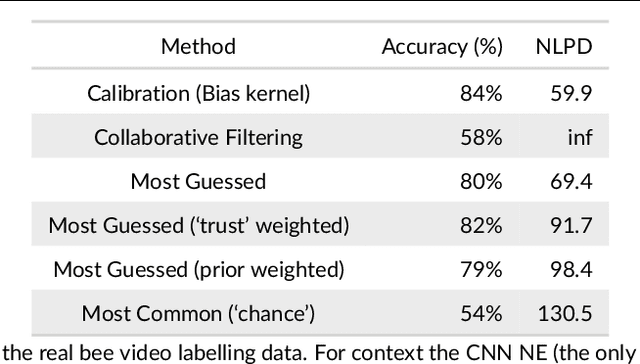
Networks of low-cost sensors are becoming ubiquitous, but often suffer from poor accuracies and drift. Regular colocation with reference sensors allows recalibration but is complicated and expensive. Alternatively the calibration can be transferred using low-cost, mobile sensors. However inferring the calibration (with uncertainty) becomes difficult. We propose a variational approach to model the calibration across the network. We demonstrate the approach on synthetic and real air pollution data, and find it can perform better than the state of the art (multi-hop calibration). We extend it to categorical data produced by citizen-scientist labelling. In Summary: The method achieves uncertainty-quantified calibration, which has been one of the barriers to low-cost sensor deployment and citizen-science research.

Sparse Gaussian process Audio Source Separation Using Spectrum Priors in the Time-Domain

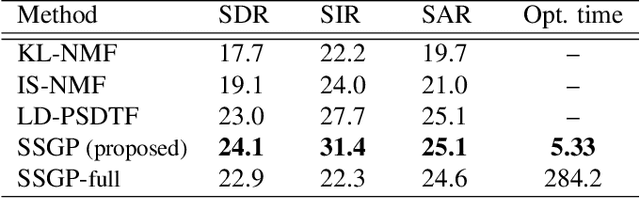
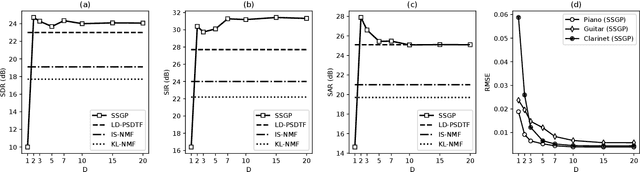
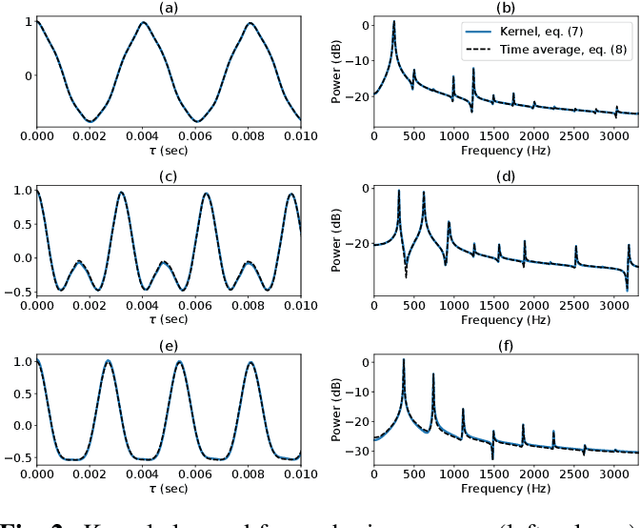
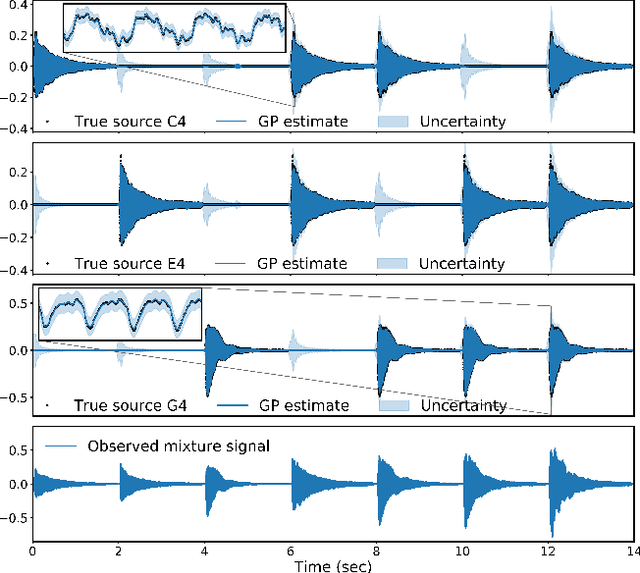
Gaussian process (GP) audio source separation is a time-domain approach that circumvents the inherent phase approximation issue of spectrogram based methods. Furthermore, through its kernel, GPs elegantly incorporate prior knowledge about the sources into the separation model. Despite these compelling advantages, the computational complexity of GP inference scales cubically with the number of audio samples. As a result, source separation GP models have been restricted to the analysis of short audio frames. We introduce an efficient application of GPs to time-domain audio source separation, without compromising performance. For this purpose, we used GP regression, together with spectral mixture kernels, and variational sparse GPs. We compared our method with LD-PSDTF (positive semi-definite tensor factorization), KL-NMF (Kullback-Leibler non-negative matrix factorization), and IS-NMF (Itakura-Saito NMF). Results show that the proposed method outperforms these techniques.

Efficient Learning of Harmonic Priors for Pitch Detection in Polyphonic Music

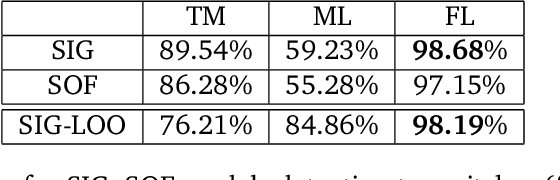
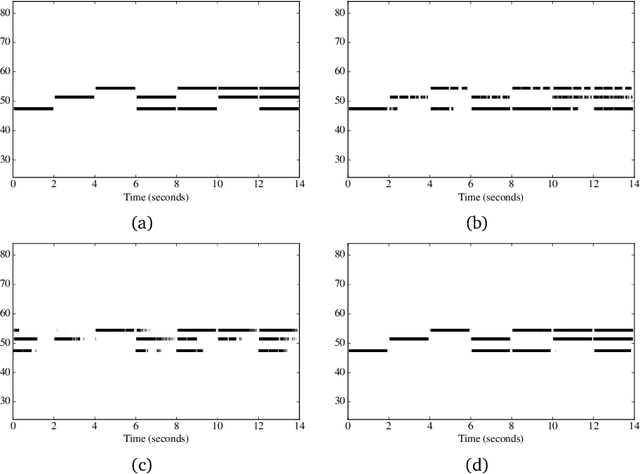
Automatic music transcription (AMT) aims to infer a latent symbolic representation of a piece of music (piano-roll), given a corresponding observed audio recording. Transcribing polyphonic music (when multiple notes are played simultaneously) is a challenging problem, due to highly structured overlapping between harmonics. We study whether the introduction of physically inspired Gaussian process (GP) priors into audio content analysis models improves the extraction of patterns required for AMT. Audio signals are described as a linear combination of sources. Each source is decomposed into the product of an amplitude-envelope, and a quasi-periodic component process. We introduce the Mat\'ern spectral mixture (MSM) kernel for describing frequency content of singles notes. We consider two different regression approaches. In the sigmoid model every pitch-activation is independently non-linear transformed. In the softmax model several activation GPs are jointly non-linearly transformed. This introduce cross-correlation between activations. We use variational Bayes for approximate inference. We empirically evaluate how these models work in practice transcribing polyphonic music. We demonstrate that rather than encourage dependency between activations, what is relevant for improving pitch detection is to learnt priors that fit the frequency content of the sound events to detect.

A Three Spatial Dimension Wave Latent Force Model for Describing Excitation Sources and Electric Potentials Produced by Deep Brain Stimulation

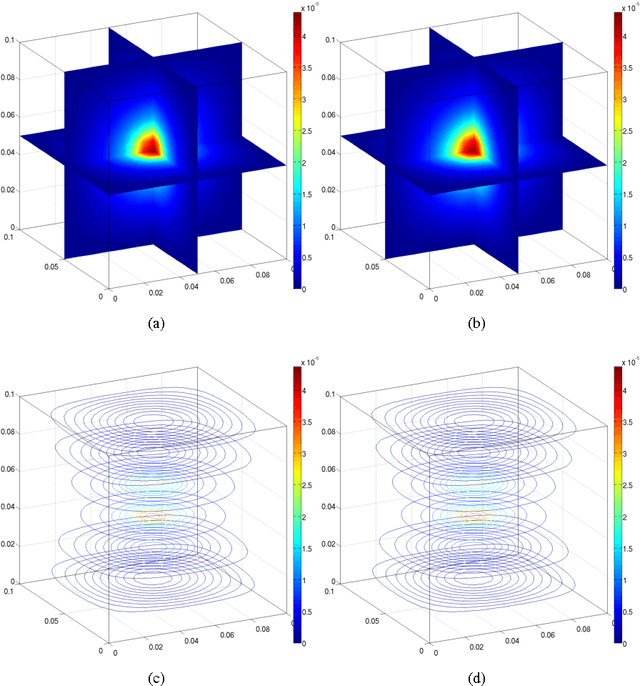
Deep brain stimulation (DBS) is a surgical treatment for Parkinson's Disease. Static models based on quasi-static approximation are common approaches for DBS modeling. While this simplification has been validated for bioelectric sources, its application to rapid stimulation pulses, which contain more high-frequency power, may not be appropriate, as DBS therapeutic results depend on stimulus parameters such as frequency and pulse width, which are related to time variations of the electric field. We propose an alternative hybrid approach based on probabilistic models and differential equations, by using Gaussian processes and wave equation. Our model avoids quasi-static approximation, moreover, it is able to describe dynamic behavior of DBS. Therefore, the proposed model may be used to obtain a more realistic phenomenon description. The proposed model can also solve inverse problems, i.e. to recover the corresponding source of excitation, given electric potential distribution. The electric potential produced by a time-varying source was predicted using proposed model. For static sources, the electric potential produced by different electrode configurations were modeled. Four different sources of excitation were recovered by solving the inverse problem. We compare our outcomes with the electric potential obtained by solving Poisson's equation using the Finite Element Method (FEM). Our approach is able to take into account time variations of the source and the produced field. Also, inverse problem can be addressed using the proposed model. The electric potential calculated with the proposed model is close to the potential obtained by solving Poisson's equation using FEM.

Gaussian Processes for Music Audio Modelling and Content Analysis

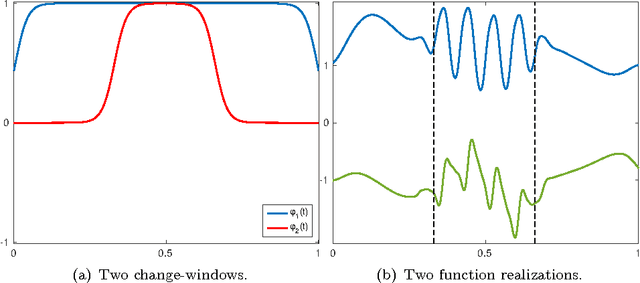
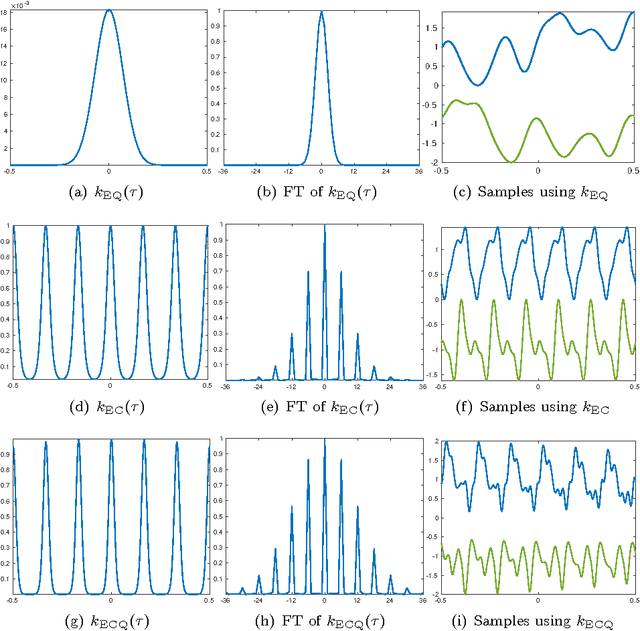
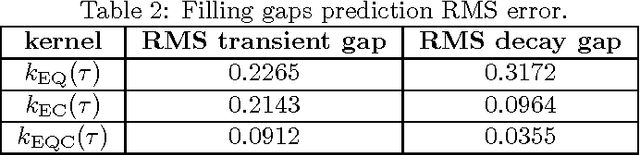
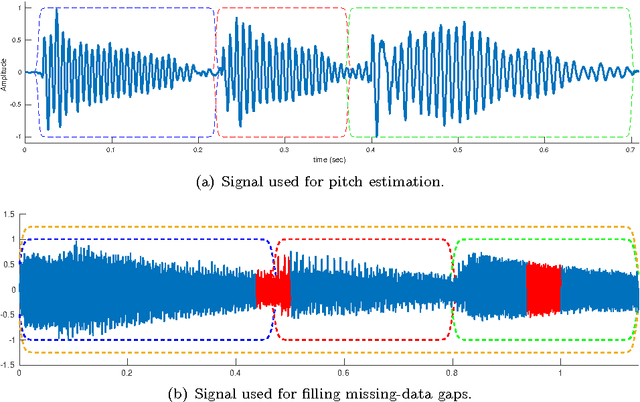
Real music signals are highly variable, yet they have strong statistical structure. Prior information about the underlying physical mechanisms by which sounds are generated and rules by which complex sound structure is constructed (notes, chords, a complete musical score), can be naturally unified using Bayesian modelling techniques. Typically algorithms for Automatic Music Transcription independently carry out individual tasks such as multiple-F0 detection and beat tracking. The challenge remains to perform joint estimation of all parameters. We present a Bayesian approach for modelling music audio, and content analysis. The proposed methodology based on Gaussian processes seeks joint estimation of multiple music concepts by incorporating into the kernel prior information about non-stationary behaviour, dynamics, and rich spectral content present in the modelled music signal. We illustrate the benefits of this approach via two tasks: pitch estimation, and inferring missing segments in a polyphonic audio recording.