Deep Learning of Causal Structures in High Dimensions

Recent years have seen rapid progress at the intersection between causality and machine learning. Motivated by scientific applications involving high-dimensional data, in particular in biomedicine, we propose a deep neural architecture for learning causal relationships between variables from a combination of empirical data and prior causal knowledge. We combine convolutional and graph neural networks within a causal risk framework to provide a flexible and scalable approach. Empirical results include linear and nonlinear simulations (where the underlying causal structures are known and can be directly compared against), as well as a real biological example where the models are applied to high-dimensional molecular data and their output compared against entirely unseen validation experiments. These results demonstrate the feasibility of using deep learning approaches to learn causal networks in large-scale problems spanning thousands of variables.

Ancestral causal learning in high dimensions with a human genome-wide application

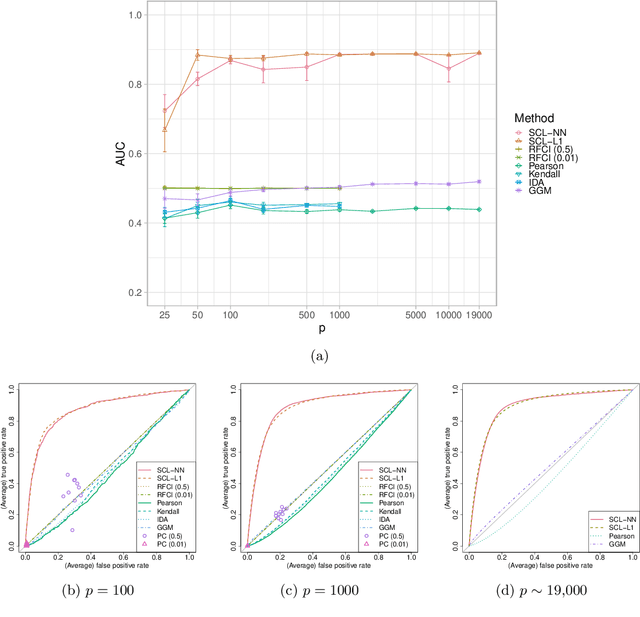
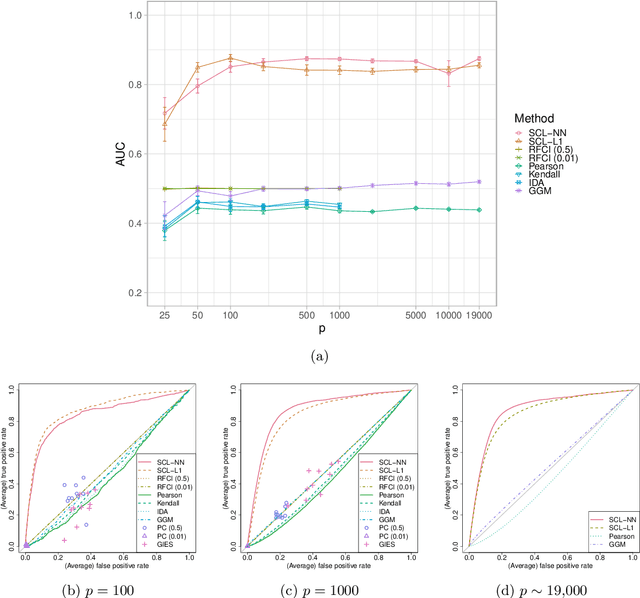
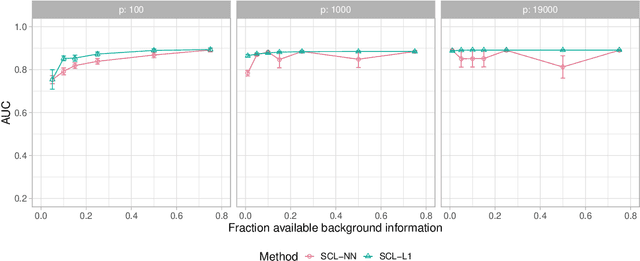
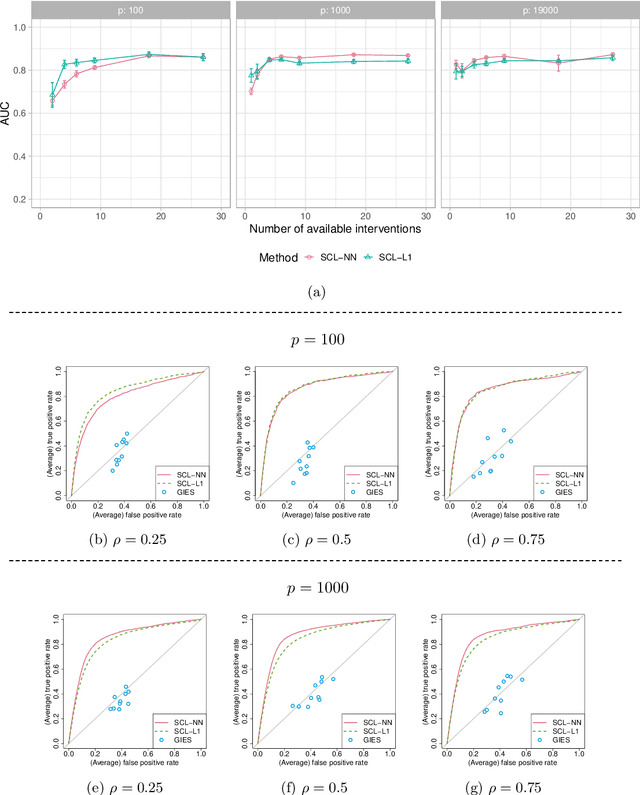
We consider learning ancestral causal relationships in high dimensions. Our approach is driven by a supervised learning perspective, with discrete indicators of causal relationships treated as labels to be learned from available data. We focus on the setting in which some causal (ancestral) relationships are known (via background knowledge or experimental data) and put forward a general approach that scales to large problems. This is motivated by problems in human biology which are characterized by high dimensionality and potentially many latent variables. We present a case study involving interventional data from human cells with total dimension $p \! \sim \! 19{,}000$. Performance is assessed empirically by testing model output against previously unseen interventional data. The proposed approach is highly effective and demonstrably scalable to the human genome-wide setting. We consider sensitivity to background knowledge and find that results are robust to nontrivial perturbations of the input information. We consider also the case, relevant to some applications, where the only prior information available concerns a small number of known ancestral relationships.

Model-based clustering in very high dimensions via adaptive projections

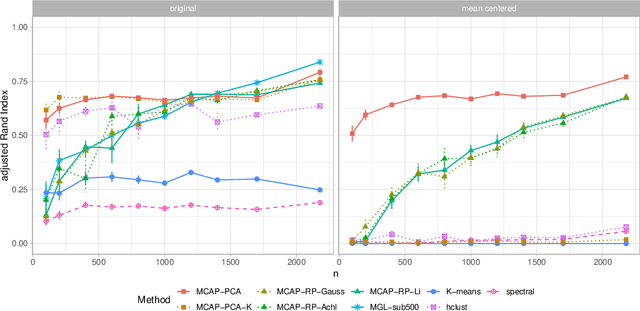
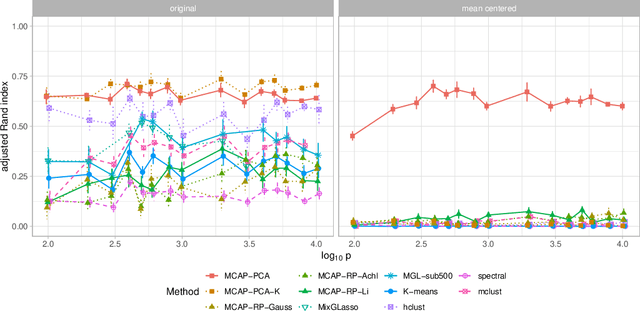
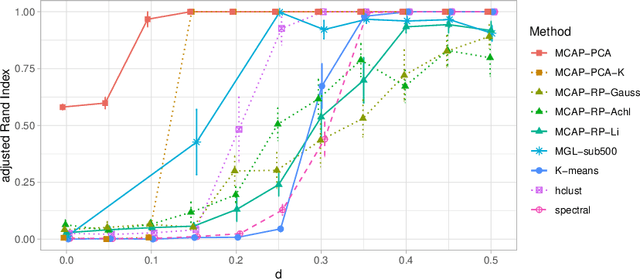
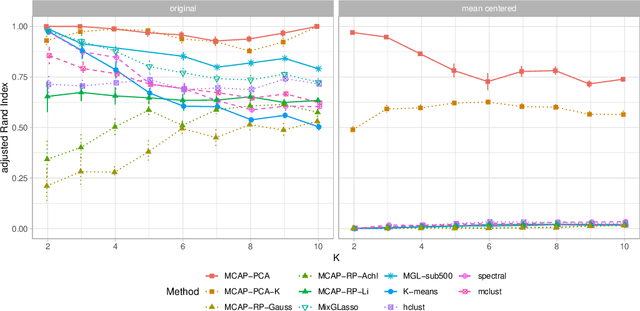
Mixture models are a standard approach to dealing with heterogeneous data with non-i.i.d. structure. However, when the dimension $p$ is large relative to sample size $n$ and where either or both of means and covariances/graphical models may differ between the latent groups, mixture models face statistical and computational difficulties and currently available methods cannot realistically go beyond $p \! \sim \! 10^4$ or so. We propose an approach called Model-based Clustering via Adaptive Projections (MCAP). Instead of estimating mixtures in the original space, we work with a low-dimensional representation obtained by linear projection. The projection dimension itself plays an important role and governs a type of bias-variance tradeoff with respect to recovery of the relevant signals. MCAP sets the projection dimension automatically in a data-adaptive manner, using a proxy for the assignment risk. Combining a full covariance formulation with the adaptive projection allows detection of both mean and covariance signals in very high dimensional problems. We show real-data examples in which covariance signals are reliably detected in problems with $p \! \sim \! 10^4$ or more, and simulations going up to $p = 10^6$. In some examples, MCAP performs well even when the mean signal is entirely removed, leaving differential covariance structure in the high-dimensional space as the only signal. Across a number of regimes, MCAP performs as well or better than a range of existing methods, including a recently-proposed $\ell_1$-penalized approach; and performance remains broadly stable with increasing dimension. MCAP can be run "out of the box" and is fast enough for interactive use on large-$p$ problems using standard desktop computing resources.