A deep learning approach to wall-shear stress quantification: From numerical training to zero-shot experimental application

The accurate quantification of wall-shear stress dynamics is of substantial importance for various applications in fundamental and applied research, spanning areas from human health to aircraft design and optimization. Despite significant progress in experimental measurement techniques and post-processing algorithms, temporally resolved wall-shear stress dynamics with adequate spatial resolution and within a suitable spatial domain remain an elusive goal. To address this gap, we introduce a deep learning architecture that ingests wall-parallel velocity fields from the logarithmic layer of turbulent wall-bounded flows and outputs the corresponding 2D wall-shear stress fields with identical spatial resolution and domain size. From a physical perspective, our framework acts as a surrogate model encapsulating the various mechanisms through which highly energetic outer-layer flow structures influence the governing wall-shear stress dynamics. The network is trained in a supervised fashion on a unified dataset comprising direct numerical simulations of statistically 1D turbulent channel and spatially developing turbulent boundary layer flows at friction Reynolds numbers ranging from 390 to 1,500. We demonstrate a zero-shot applicability to experimental velocity fields obtained from Particle-Image Velocimetry measurements and verify the physical accuracy of the wall-shear stress estimates with synchronized wall-shear stress measurements using the Micro-Pillar Shear-Stress Sensor for Reynolds numbers up to 2,000. In summary, the presented framework lays the groundwork for extracting inaccessible experimental wall-shear stress information from readily available velocity measurements and thus, facilitates advancements in a variety of experimental applications.

Uncovering wall-shear stress dynamics from neural-network enhanced fluid flow measurements

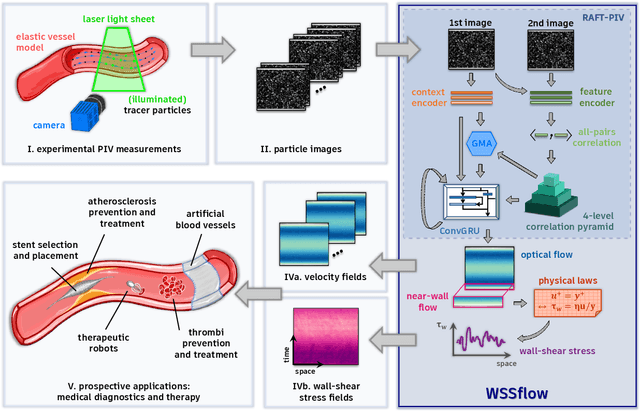
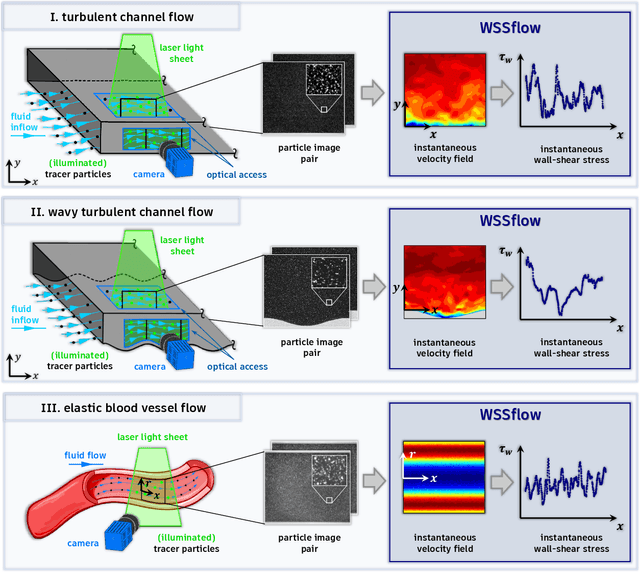
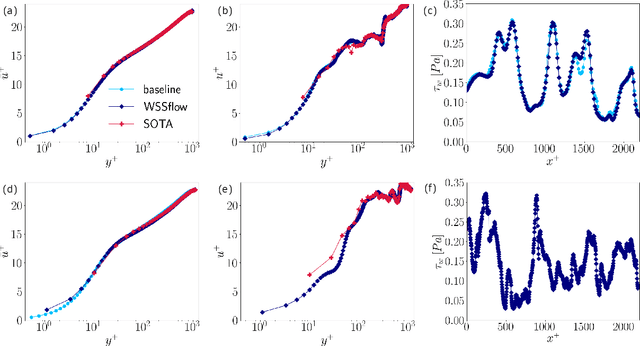
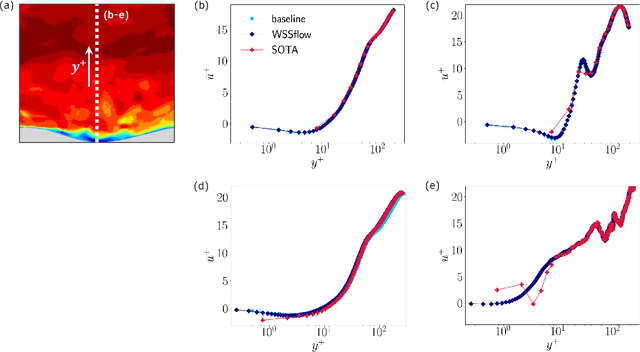
Friction drag from a turbulent fluid moving past or inside an object plays a crucial role in domains as diverse as transportation, public utility infrastructure, energy technology, and human health. As a direct measure of the shear-induced friction forces, an accurate prediction of the wall-shear stress can contribute to sustainability, conservation of resources, and carbon neutrality in civil aviation as well as enhanced medical treatment of vascular diseases and cancer. Despite such importance for our modern society, we still lack adequate experimental methods to capture the instantaneous wall-shear stress dynamics. In this contribution, we present a holistic approach that derives velocity and wall-shear stress fields with impressive spatial and temporal resolution from flow measurements using a deep optical flow estimator with physical knowledge. The validity and physical correctness of the derived flow quantities is demonstrated with synthetic and real-world experimental data covering a range of relevant fluid flows.

Learning Latent Dynamics via Invariant Decomposition and (Spatio-)Temporal Transformers

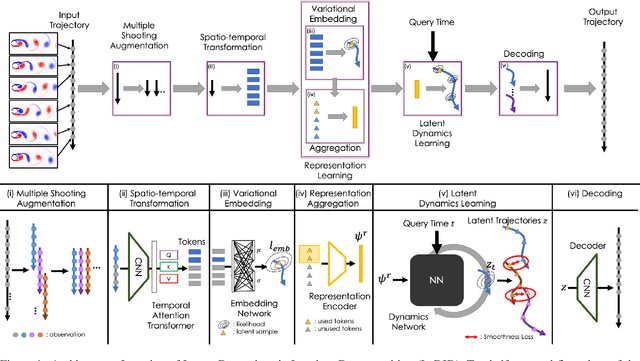
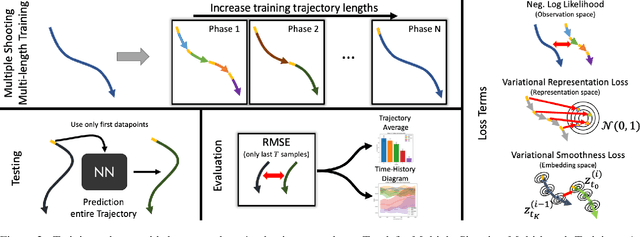
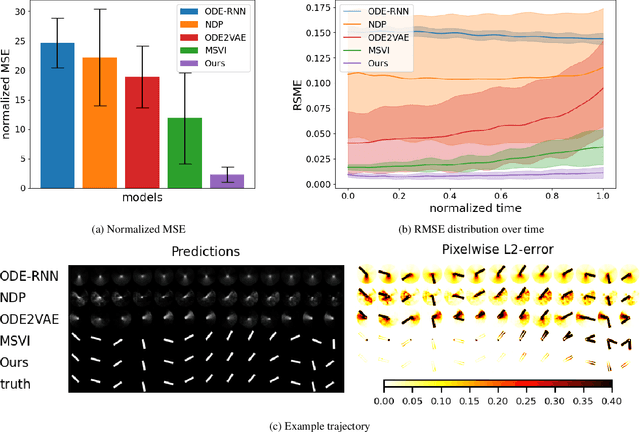
We propose a method for learning dynamical systems from high-dimensional empirical data that combines variational autoencoders and (spatio-)temporal attention within a framework designed to enforce certain scientifically-motivated invariances. We focus on the setting in which data are available from multiple different instances of a system whose underlying dynamical model is entirely unknown at the outset. The approach rests on a separation into an instance-specific encoding (capturing initial conditions, constants etc.) and a latent dynamics model that is itself universal across all instances/realizations of the system. The separation is achieved in an automated, data-driven manner and only empirical data are required as inputs to the model. The approach allows effective inference of system behaviour at any continuous time but does not require an explicit neural ODE formulation, which makes it efficient and highly scalable. We study behaviour through simple theoretical analyses and extensive experiments on synthetic and real-world datasets. The latter investigate learning the dynamics of complex systems based on finite data and show that the proposed approach can outperform state-of-the-art neural-dynamical models. We study also more general inductive bias in the context of transfer to data obtained under entirely novel system interventions. Overall, our results provide a promising new framework for efficiently learning dynamical models from heterogeneous data with potential applications in a wide range of fields including physics, medicine, biology and engineering.

Deep Learning of Causal Structures in High Dimensions

Recent years have seen rapid progress at the intersection between causality and machine learning. Motivated by scientific applications involving high-dimensional data, in particular in biomedicine, we propose a deep neural architecture for learning causal relationships between variables from a combination of empirical data and prior causal knowledge. We combine convolutional and graph neural networks within a causal risk framework to provide a flexible and scalable approach. Empirical results include linear and nonlinear simulations (where the underlying causal structures are known and can be directly compared against), as well as a real biological example where the models are applied to high-dimensional molecular data and their output compared against entirely unseen validation experiments. These results demonstrate the feasibility of using deep learning approaches to learn causal networks in large-scale problems spanning thousands of variables.