Model-based clustering in very high dimensions via adaptive projections
Paper and Code
Feb 22, 2019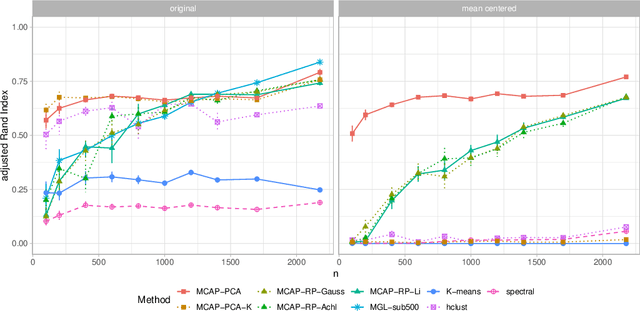
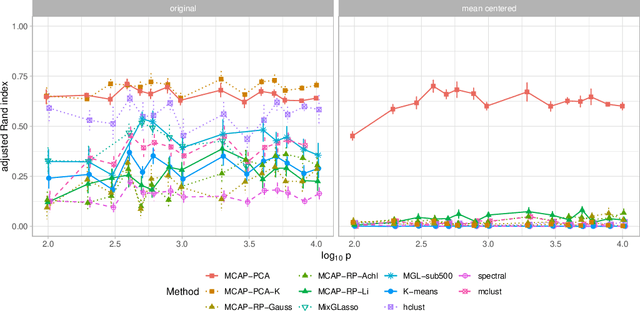
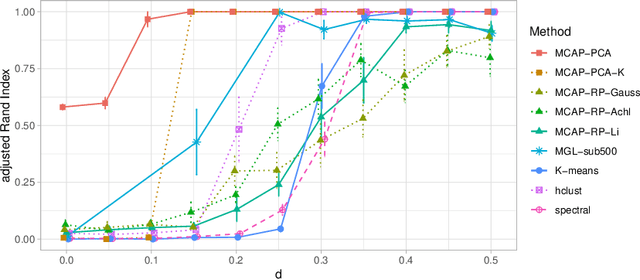
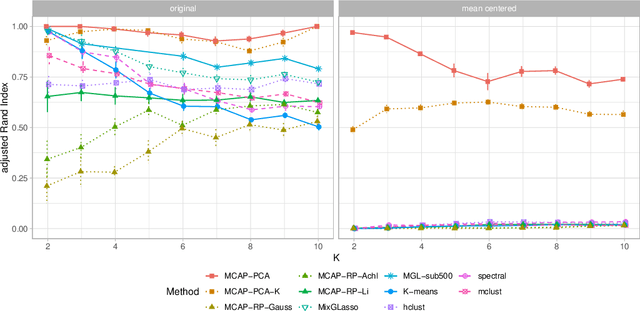
Mixture models are a standard approach to dealing with heterogeneous data with non-i.i.d. structure. However, when the dimension $p$ is large relative to sample size $n$ and where either or both of means and covariances/graphical models may differ between the latent groups, mixture models face statistical and computational difficulties and currently available methods cannot realistically go beyond $p \! \sim \! 10^4$ or so. We propose an approach called Model-based Clustering via Adaptive Projections (MCAP). Instead of estimating mixtures in the original space, we work with a low-dimensional representation obtained by linear projection. The projection dimension itself plays an important role and governs a type of bias-variance tradeoff with respect to recovery of the relevant signals. MCAP sets the projection dimension automatically in a data-adaptive manner, using a proxy for the assignment risk. Combining a full covariance formulation with the adaptive projection allows detection of both mean and covariance signals in very high dimensional problems. We show real-data examples in which covariance signals are reliably detected in problems with $p \! \sim \! 10^4$ or more, and simulations going up to $p = 10^6$. In some examples, MCAP performs well even when the mean signal is entirely removed, leaving differential covariance structure in the high-dimensional space as the only signal. Across a number of regimes, MCAP performs as well or better than a range of existing methods, including a recently-proposed $\ell_1$-penalized approach; and performance remains broadly stable with increasing dimension. MCAP can be run "out of the box" and is fast enough for interactive use on large-$p$ problems using standard desktop computing resources.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge