Scalable Multi-Output Gaussian Processes with Stochastic Variational Inference

The Multi-Output Gaussian Process is is a popular tool for modelling data from multiple sources. A typical choice to build a covariance function for a MOGP is the Linear Model of Coregionalization (LMC) which parametrically models the covariance between outputs. The Latent Variable MOGP (LV-MOGP) generalises this idea by modelling the covariance between outputs using a kernel applied to latent variables, one per output, leading to a flexible MOGP model that allows efficient generalization to new outputs with few data points. Computational complexity in LV-MOGP grows linearly with the number of outputs, which makes it unsuitable for problems with a large number of outputs. In this paper, we propose a stochastic variational inference approach for the LV-MOGP that allows mini-batches for both inputs and outputs, making computational complexity per training iteration independent of the number of outputs.

Fast nonparametric clustering of structured time-series

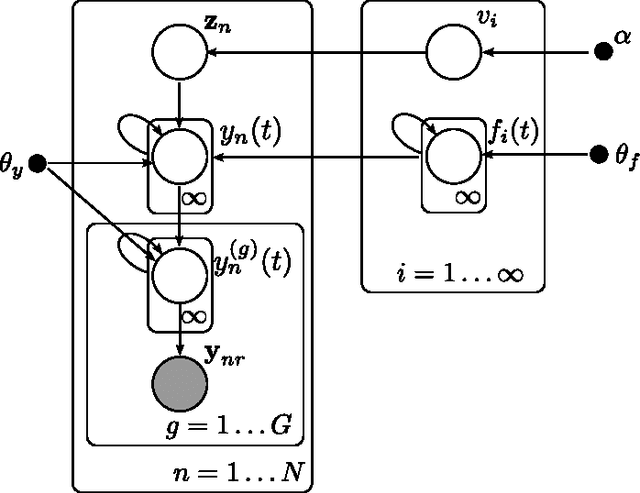
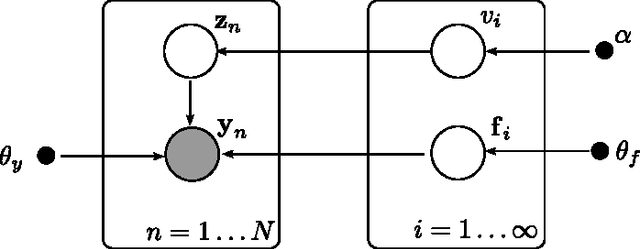
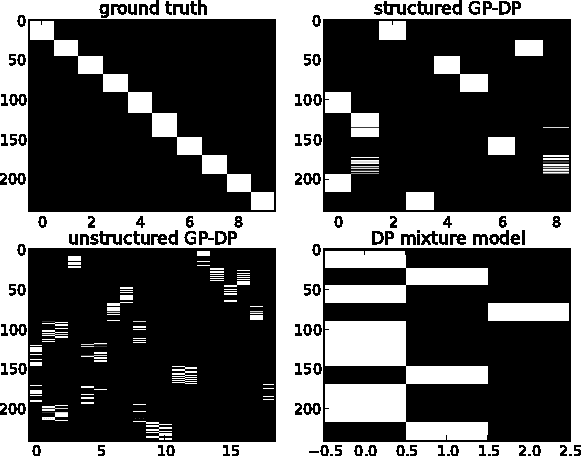
In this publication, we combine two Bayesian non-parametric models: the Gaussian Process (GP) and the Dirichlet Process (DP). Our innovation in the GP model is to introduce a variation on the GP prior which enables us to model structured time-series data, i.e. data containing groups where we wish to model inter- and intra-group variability. Our innovation in the DP model is an implementation of a new fast collapsed variational inference procedure which enables us to optimize our variationala pproximation significantly faster than standard VB approaches. In a biological time series application we show how our model better captures salient features of the data, leading to better consistency with existing biological classifications, while the associated inference algorithm provides a twofold speed-up over EM-based variational inference.

Fast Variational Inference in the Conjugate Exponential Family

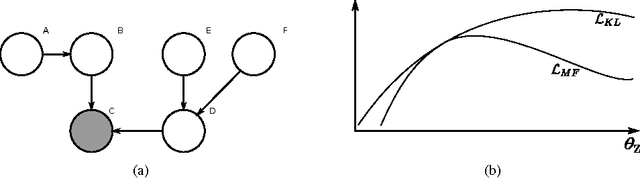
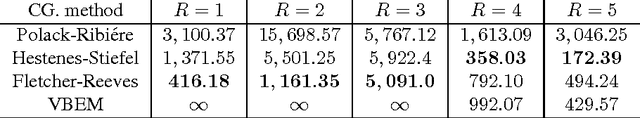
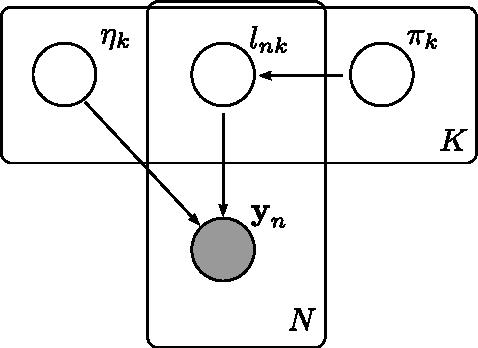
We present a general method for deriving collapsed variational inference algo- rithms for probabilistic models in the conjugate exponential family. Our method unifies many existing approaches to collapsed variational inference. Our collapsed variational inference leads to a new lower bound on the marginal likelihood. We exploit the information geometry of the bound to derive much faster optimization methods based on conjugate gradients for these models. Our approach is very general and is easily applied to any model where the mean field update equations have been derived. Empirically we show significant speed-ups for probabilistic models optimized using our bound.