Transforming Heart Chamber Imaging: Self-Supervised Learning for Whole Heart Reconstruction and Segmentation

Automated segmentation of Cardiac Magnetic Resonance (CMR) plays a pivotal role in efficiently assessing cardiac function, offering rapid clinical evaluations that benefit both healthcare practitioners and patients. While recent research has primarily focused on delineating structures in the short-axis orientation, less attention has been given to long-axis representations, mainly due to the complex nature of structures in this orientation. Performing pixel-wise segmentation of the left ventricular (LV) myocardium and the four cardiac chambers in 2-D steady-state free precession (SSFP) cine sequences is a crucial preprocessing stage for various analyses. However, the challenge lies in the significant variability in contrast, appearance, orientation, and positioning of the heart across different patients, clinical views, scanners, and imaging protocols. Consequently, achieving fully automatic semantic segmentation in this context is notoriously challenging. In recent years, several deep learning models have been proposed to accurately quantify and diagnose cardiac pathologies. These automated tools heavily rely on the accurate segmentation of cardiac structures in magnetic resonance images (MRI). Hence, there is a need for new methods to handle such structures' geometrical and textural complexities. We proposed 2D and 3D two-stage self-supervised deep learning segmentation hybrid transformer and CNN-based architectures for 4CH whole heart segmentation. Accurate segmentation of the ventricles and atria in 4CH views is crucial for analyzing heart health and reconstructing four-chamber meshes, which are essential for estimating various parameters to assess overall heart condition. Our proposed method outperformed state-of-the-art techniques, demonstrating superior performance in this domain.

Adjoint-aided inference of Gaussian process driven differential equations

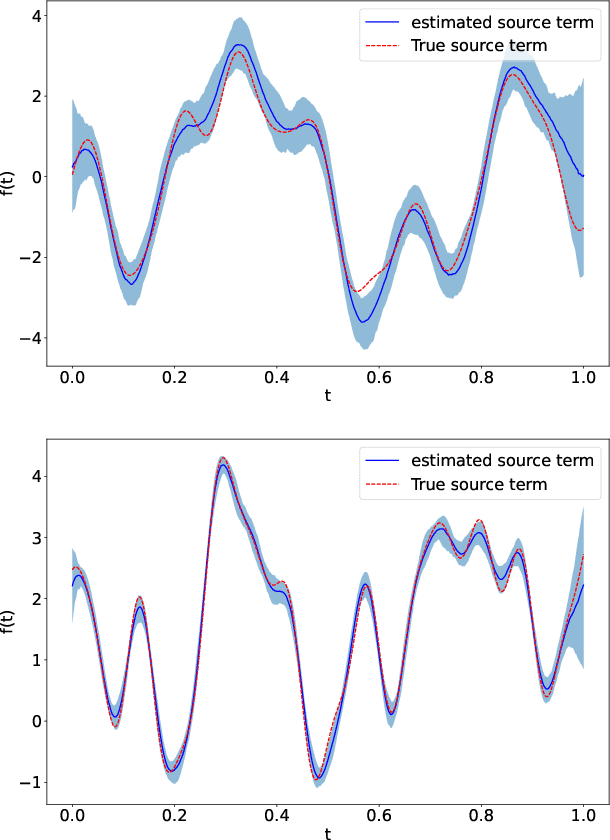
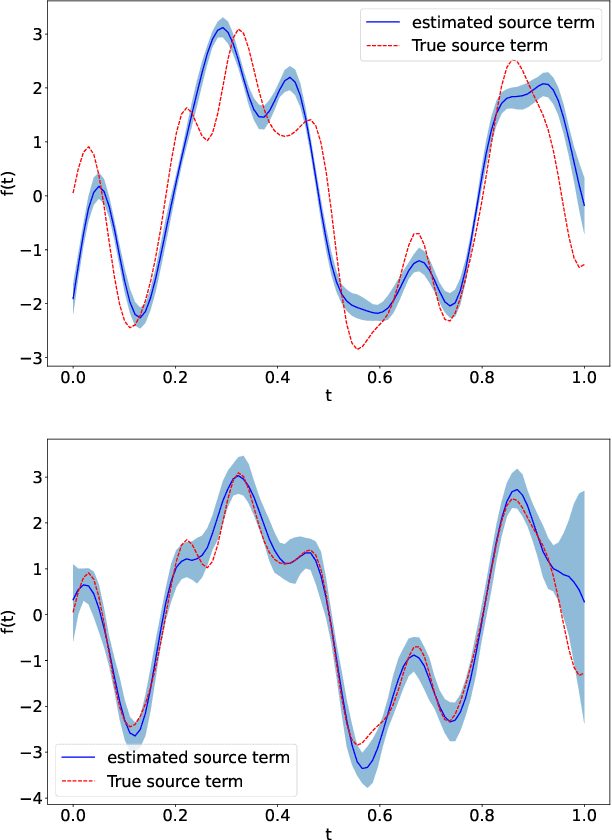
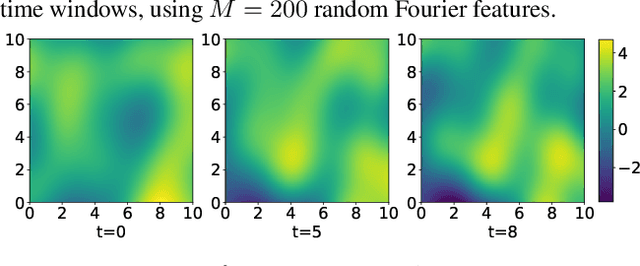
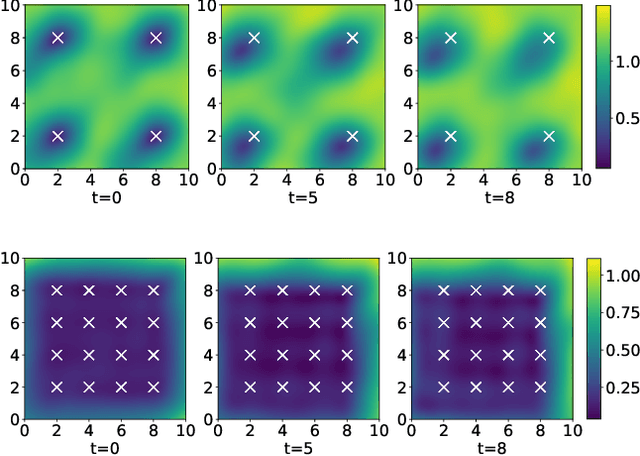
Linear systems occur throughout engineering and the sciences, most notably as differential equations. In many cases the forcing function for the system is unknown, and interest lies in using noisy observations of the system to infer the forcing, as well as other unknown parameters. In differential equations, the forcing function is an unknown function of the independent variables (typically time and space), and can be modelled as a Gaussian process (GP). In this paper we show how the adjoint of a linear system can be used to efficiently infer forcing functions modelled as GPs, after using a truncated basis expansion of the GP kernel. We show how exact conjugate Bayesian inference for the truncated GP can be achieved, in many cases with substantially lower computation than would be required using MCMC methods. We demonstrate the approach on systems of both ordinary and partial differential equations, and by testing on synthetic data, show that the basis expansion approach approximates well the true forcing with a modest number of basis vectors. Finally, we show how to infer point estimates for the non-linear model parameters, such as the kernel length-scales, using Bayesian optimisation.

Considering discrepancy when calibrating a mechanistic electrophysiology model

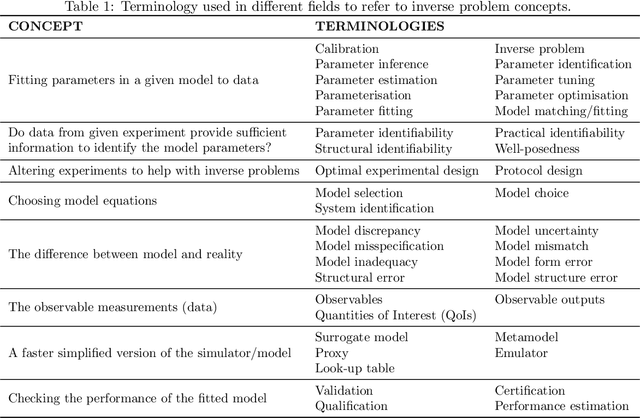
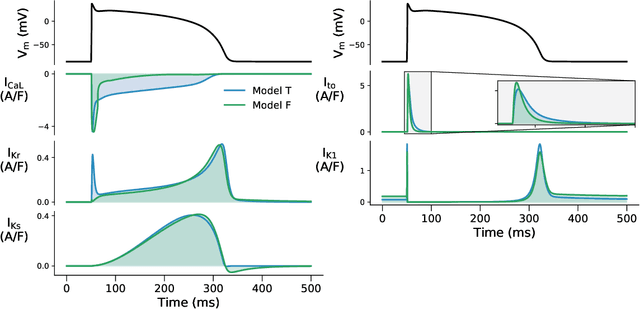
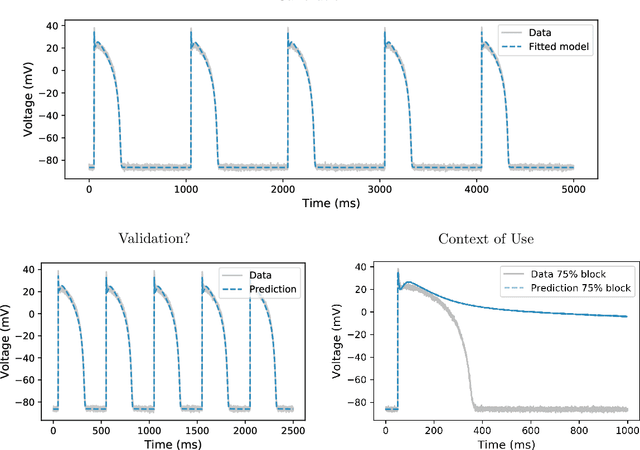
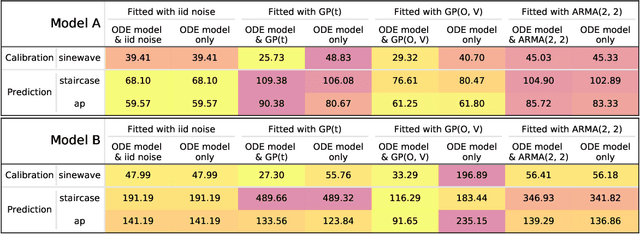
Uncertainty quantification (UQ) is a vital step in using mathematical models and simulations to take decisions. The field of cardiac simulation has begun to explore and adopt UQ methods to characterise uncertainty in model inputs and how that propagates through to outputs or predictions. In this perspective piece we draw attention to an important and under-addressed source of uncertainty in our predictions --- that of uncertainty in the model structure or the equations themselves. The difference between imperfect models and reality is termed model discrepancy, and we are often uncertain as to the size and consequences of this discrepancy. Here we provide two examples of the consequences of discrepancy when calibrating models at the ion channel and action potential scales. Furthermore, we attempt to account for this discrepancy when calibrating and validating an ion channel model using different methods, based on modelling the discrepancy using Gaussian processes (GPs) and autoregressive-moving-average (ARMA) models, then highlight the advantages and shortcomings of each approach. Finally, suggestions and lines of enquiry for future work are provided.