Estimating Cardiac Tissue Conductivity from Electrograms with Fully Convolutional Networks

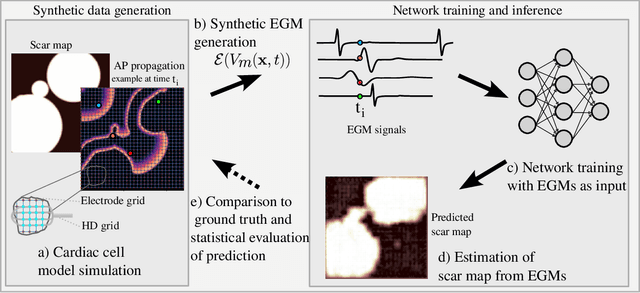
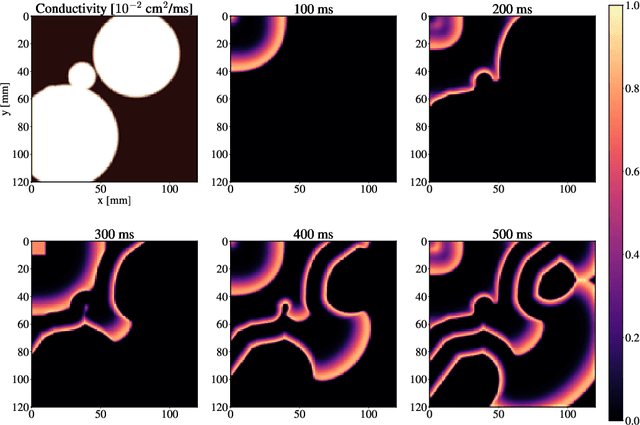
Atrial Fibrillation (AF) is characterized by disorganised electrical activity in the atria and is known to be sustained by the presence of regions of fibrosis (scars) or functional cellular remodeling, both of which may lead to areas of slow conduction. Estimating the effective conductivity of the myocardium and identifying regions of abnormal propagation is therefore crucial for the effective treatment of AF. We hypothesise that the spatial distribution of tissue conductivity can be directly inferred from an array of concurrently acquired contact electrograms (EGMs). We generate a dataset of simulated cardiac AP propagation using randomised scar distributions and a phenomenological cardiac model and calculate contact electrograms at various positions on the field. A deep neural network, based on a modified U-net architecture, is trained to estimate the location of the scar and quantify conductivity of the tissue with a Jaccard index of $91$%. We adapt a wavelet-based surrogate testing analysis to confirm that the inferred conductivity distribution is an accurate representation of the ground truth input to the model. We find that the root mean square error (RMSE) between the ground truth and our predictions is significantly smaller ($p_{val}=0.007$) than the RMSE between the ground truth and surrogate samples.

Considering discrepancy when calibrating a mechanistic electrophysiology model

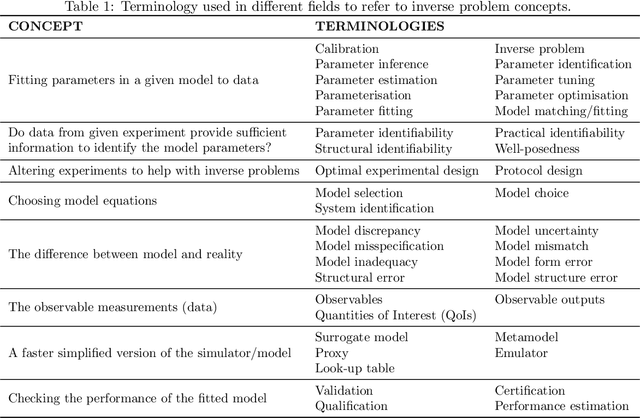
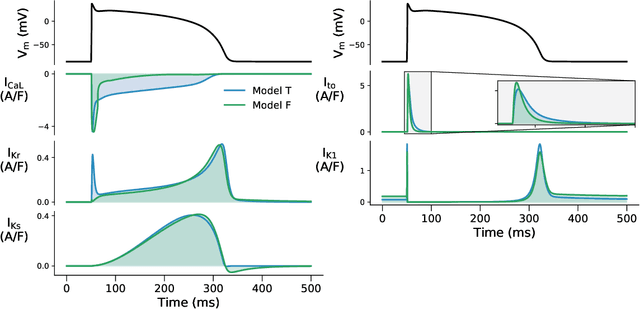
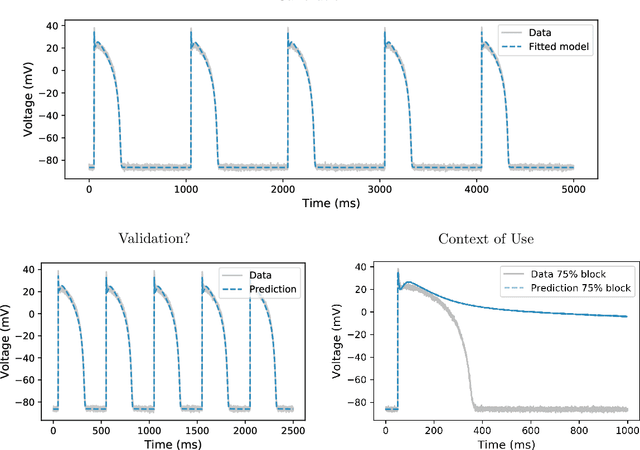
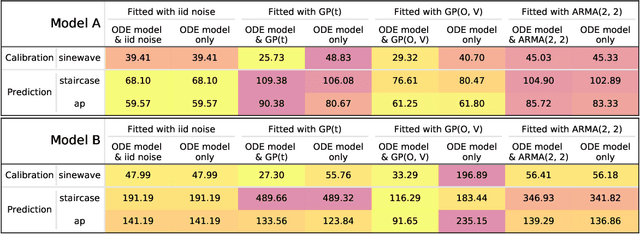
Uncertainty quantification (UQ) is a vital step in using mathematical models and simulations to take decisions. The field of cardiac simulation has begun to explore and adopt UQ methods to characterise uncertainty in model inputs and how that propagates through to outputs or predictions. In this perspective piece we draw attention to an important and under-addressed source of uncertainty in our predictions --- that of uncertainty in the model structure or the equations themselves. The difference between imperfect models and reality is termed model discrepancy, and we are often uncertain as to the size and consequences of this discrepancy. Here we provide two examples of the consequences of discrepancy when calibrating models at the ion channel and action potential scales. Furthermore, we attempt to account for this discrepancy when calibrating and validating an ion channel model using different methods, based on modelling the discrepancy using Gaussian processes (GPs) and autoregressive-moving-average (ARMA) models, then highlight the advantages and shortcomings of each approach. Finally, suggestions and lines of enquiry for future work are provided.

Approximating the solution to wave propagation using deep neural networks

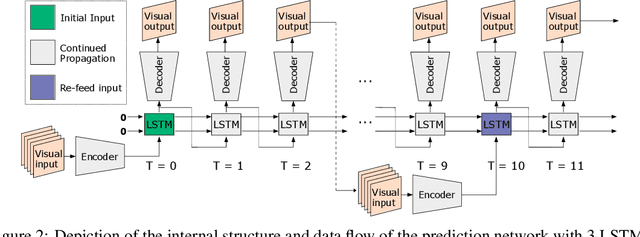
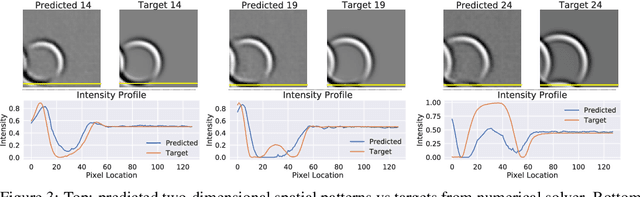
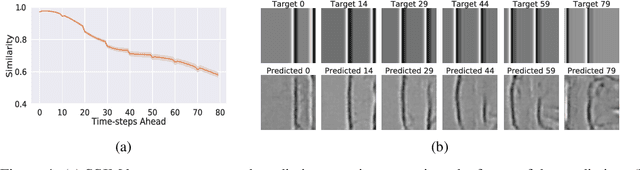
Humans gain an implicit understanding of physical laws through observing and interacting with the world. Endowing an autonomous agent with an understanding of physical laws through experience and observation is seldom practical: we should seek alternatives. Fortunately, many of the laws of behaviour of the physical world can be derived from prior knowledge of dynamical systems, expressed through the use of partial differential equations. In this work, we suggest a neural network capable of understanding a specific physical phenomenon: wave propagation in a two-dimensional medium. We define `understanding' in this context as the ability to predict the future evolution of the spatial patterns of rendered wave amplitude from a relatively small set of initial observations. The inherent complexity of the wave equations -- together with the existence of reflections and interference -- makes the prediction problem non-trivial. A network capable of making approximate predictions also unlocks the opportunity to speed-up numerical simulations for wave propagation. To this aim, we created a novel dataset of simulated wave motion and built a predictive deep neural network comprising of three main blocks: an encoder, a propagator made by 3 LSTMs, and a decoder. Results show reasonable predictions for as long as 80 time steps into the future on a dataset not seen during training. Furthermore, the network is able to generalize to an initial condition that is qualitatively different from those seen during training.

Rethinking multiscale cardiac electrophysiology with machine learning and predictive modelling

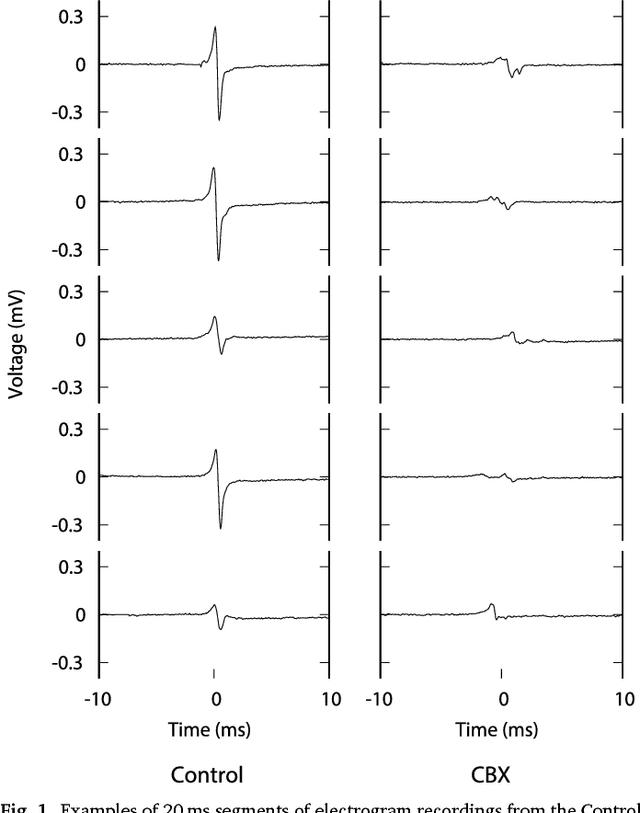
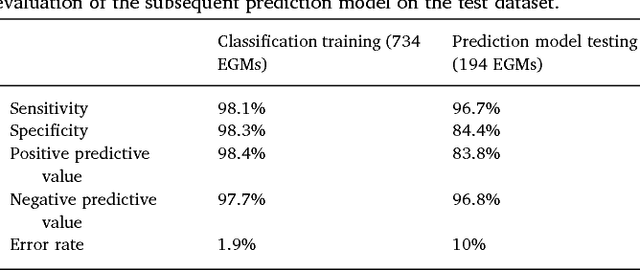
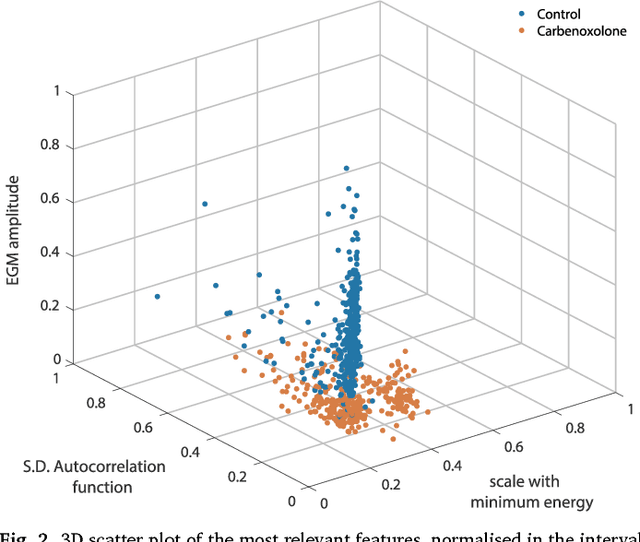
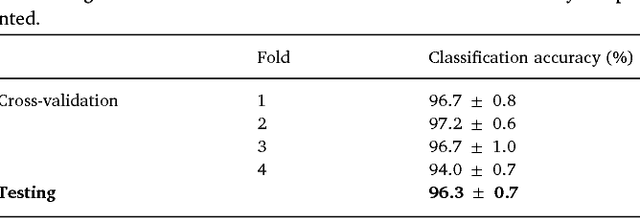
We review some of the latest approaches to analysing cardiac electrophysiology data using machine learning and predictive modelling. Cardiac arrhythmias, particularly atrial fibrillation, are a major global healthcare challenge. Treatment is often through catheter ablation, which involves the targeted localized destruction of regions of the myocardium responsible for initiating or perpetuating the arrhythmia. Ablation targets are either anatomically defined, or identified based on their functional properties as determined through the analysis of contact intracardiac electrograms acquired with increasing spatial density by modern electroanatomic mapping systems. While numerous quantitative approaches have been investigated over the past decades for identifying these critical curative sites, few have provided a reliable and reproducible advance in success rates. Machine learning techniques, including recent deep-learning approaches, offer a potential route to gaining new insight from this wealth of highly complex spatio-temporal information that existing methods struggle to analyse. Coupled with predictive modelling, these techniques offer exciting opportunities to advance the field and produce more accurate diagnoses and robust personalised treatment. We outline some of these methods and illustrate their use in making predictions from the contact electrogram and augmenting predictive modelling tools, both by more rapidly predicting future states of the system and by inferring the parameters of these models from experimental observations.