BATseg: Boundary-aware Multiclass Spinal Cord Tumor Segmentation on 3D MRI Scans

Spinal cord tumors significantly contribute to neurological morbidity and mortality. Precise morphometric quantification, encompassing the size, location, and type of such tumors, holds promise for optimizing treatment planning strategies. Although recent methods have demonstrated excellent performance in medical image segmentation, they primarily focus on discerning shapes with relatively large morphology such as brain tumors, ignoring the challenging problem of identifying spinal cord tumors which tend to have tiny sizes, diverse locations, and shapes. To tackle this hard problem of multiclass spinal cord tumor segmentation, we propose a new method, called BATseg, to learn a tumor surface distance field by applying our new multiclass boundary-aware loss function. To verify the effectiveness of our approach, we also introduce the first and large-scale spinal cord tumor dataset. It comprises gadolinium-enhanced T1-weighted 3D MRI scans from 653 patients and contains the four most common spinal cord tumor types: astrocytomas, ependymomas, hemangioblastomas, and spinal meningiomas. Extensive experiments on our dataset and another public kidney tumor segmentation dataset show that our proposed method achieves superior performance for multiclass tumor segmentation.

Model Evidence with Fast Tree Based Quadrature

High dimensional integration is essential to many areas of science, ranging from particle physics to Bayesian inference. Approximating these integrals is hard, due in part to the difficulty of locating and sampling from regions of the integration domain that make significant contributions to the overall integral. Here, we present a new algorithm called Tree Quadrature (TQ) that separates this sampling problem from the problem of using those samples to produce an approximation of the integral. TQ places no qualifications on how the samples provided to it are obtained, allowing it to use state-of-the-art sampling algorithms that are largely ignored by existing integration algorithms. Given a set of samples, TQ constructs a surrogate model of the integrand in the form of a regression tree, with a structure optimised to maximise integral precision. The tree divides the integration domain into smaller containers, which are individually integrated and aggregated to estimate the overall integral. Any method can be used to integrate each individual container, so existing integration methods, like Bayesian Monte Carlo, can be combined with TQ to boost their performance. On a set of benchmark problems, we show that TQ provides accurate approximations to integrals in up to 15 dimensions; and in dimensions 4 and above, it outperforms simple Monte Carlo and the popular Vegas method.

Considering discrepancy when calibrating a mechanistic electrophysiology model

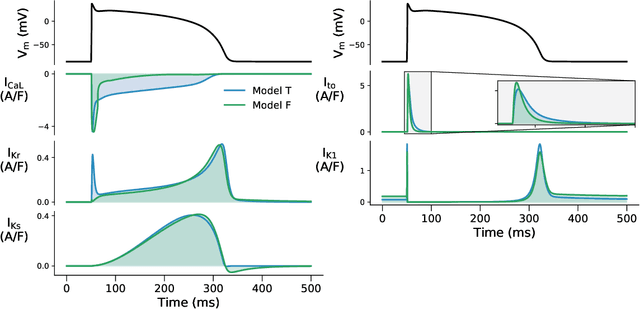
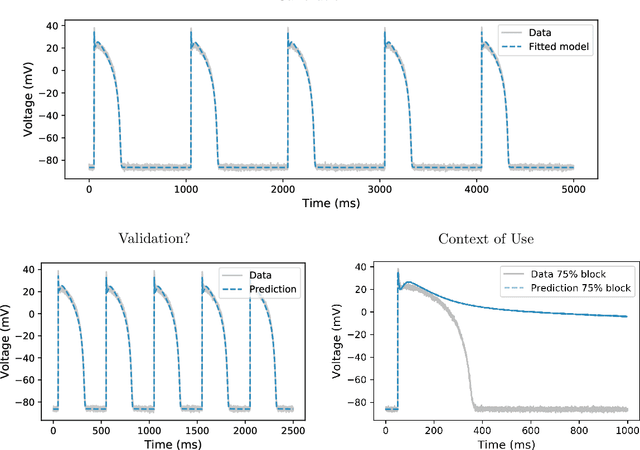
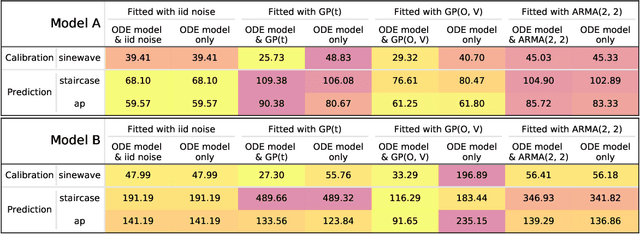
Uncertainty quantification (UQ) is a vital step in using mathematical models and simulations to take decisions. The field of cardiac simulation has begun to explore and adopt UQ methods to characterise uncertainty in model inputs and how that propagates through to outputs or predictions. In this perspective piece we draw attention to an important and under-addressed source of uncertainty in our predictions --- that of uncertainty in the model structure or the equations themselves. The difference between imperfect models and reality is termed model discrepancy, and we are often uncertain as to the size and consequences of this discrepancy. Here we provide two examples of the consequences of discrepancy when calibrating models at the ion channel and action potential scales. Furthermore, we attempt to account for this discrepancy when calibrating and validating an ion channel model using different methods, based on modelling the discrepancy using Gaussian processes (GPs) and autoregressive-moving-average (ARMA) models, then highlight the advantages and shortcomings of each approach. Finally, suggestions and lines of enquiry for future work are provided.