Compute as Teacher: Turning Inference Compute Into Reference-Free Supervision

Where do learning signals come from when there is no ground truth in post-training? We propose turning exploration into supervision through Compute as Teacher (CaT), which converts the model's own exploration at inference-time into reference-free supervision by synthesizing a single reference from a group of parallel rollouts and then optimizing toward it. Concretely, the current policy produces a group of rollouts; a frozen anchor (the initial policy) reconciles omissions and contradictions to estimate a reference, turning extra inference-time compute into a teacher signal. We turn this into rewards in two regimes: (i) verifiable tasks use programmatic equivalence on final answers; (ii) non-verifiable tasks use self-proposed rubrics-binary, auditable criteria scored by an independent LLM judge, with reward given by the fraction satisfied. Unlike selection methods (best-of-N, majority, perplexity, or judge scores), synthesis may disagree with the majority and be correct even when all rollouts are wrong; performance scales with the number of rollouts. As a test-time procedure, CaT improves Gemma 3 4B, Qwen 3 4B, and Llama 3.1 8B (up to +27% on MATH-500; +12% on HealthBench). With reinforcement learning (CaT-RL), we obtain further gains (up to +33% and +30%), with the trained policy surpassing the initial teacher signal.

Learning to Reason at the Frontier of Learnability

Reinforcement learning is now widely adopted as the final stage of large language model training, especially for reasoning-style tasks such as maths problems. Typically, models attempt each question many times during a single training step and attempt to learn from their successes and failures. However, we demonstrate that throughout training with two popular algorithms (PPO and VinePPO) on two widely used datasets, many questions are either solved by all attempts - meaning they are already learned - or by none - providing no meaningful training signal. To address this, we adapt a method from the reinforcement learning literature - sampling for learnability - and apply it to the reinforcement learning stage of LLM training. Our curriculum prioritises questions with high variance of success, i.e. those where the agent sometimes succeeds, but not always. Our findings demonstrate that this curriculum consistently boosts training performance across multiple algorithms and datasets, paving the way for more efficient and effective reinforcement learning in LLMs.

Flexible visual prompts for in-context learning in computer vision

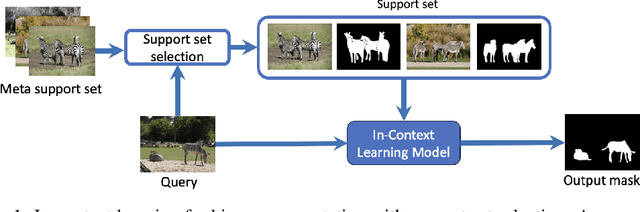
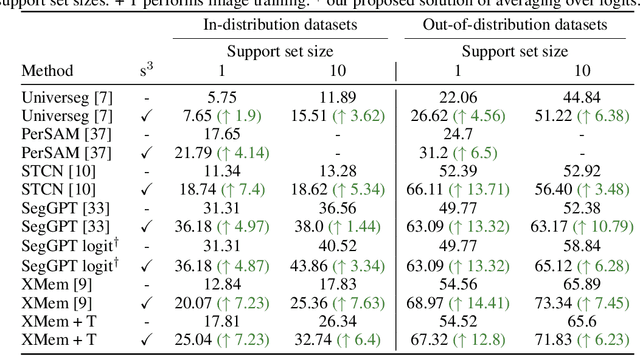
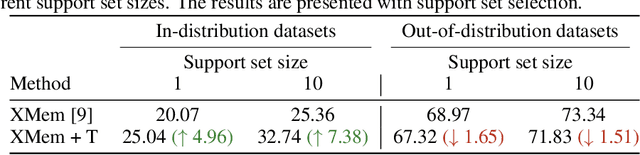
In this work, we address in-context learning (ICL) for the task of image segmentation, introducing a novel approach that adapts a modern Video Object Segmentation (VOS) technique for visual in-context learning. This adaptation is inspired by the VOS method's ability to efficiently and flexibly learn objects from a few examples. Through evaluations across a range of support set sizes and on diverse segmentation datasets, our method consistently surpasses existing techniques. Notably, it excels with data containing classes not encountered during training. Additionally, we propose a technique for support set selection, which involves choosing the most relevant images to include in this set. By employing support set selection, the performance increases for all tested methods without the need for additional training or prompt tuning. The code can be found at https://github.com/v7labs/XMem_ICL/.

Model Evidence with Fast Tree Based Quadrature

High dimensional integration is essential to many areas of science, ranging from particle physics to Bayesian inference. Approximating these integrals is hard, due in part to the difficulty of locating and sampling from regions of the integration domain that make significant contributions to the overall integral. Here, we present a new algorithm called Tree Quadrature (TQ) that separates this sampling problem from the problem of using those samples to produce an approximation of the integral. TQ places no qualifications on how the samples provided to it are obtained, allowing it to use state-of-the-art sampling algorithms that are largely ignored by existing integration algorithms. Given a set of samples, TQ constructs a surrogate model of the integrand in the form of a regression tree, with a structure optimised to maximise integral precision. The tree divides the integration domain into smaller containers, which are individually integrated and aggregated to estimate the overall integral. Any method can be used to integrate each individual container, so existing integration methods, like Bayesian Monte Carlo, can be combined with TQ to boost their performance. On a set of benchmark problems, we show that TQ provides accurate approximations to integrals in up to 15 dimensions; and in dimensions 4 and above, it outperforms simple Monte Carlo and the popular Vegas method.