Correcting Predictions for Approximate Bayesian Inference

Bayesian models quantify uncertainty and facilitate optimal decision-making in downstream applications. For most models, however, practitioners are forced to use approximate inference techniques that lead to sub-optimal decisions due to incorrect posterior predictive distributions. We present a novel approach that corrects for inaccuracies in posterior inference by altering the decision-making process. We train a separate model to make optimal decisions under the approximate posterior, combining interpretable Bayesian modeling with optimization of direct predictive accuracy in a principled fashion. The solution is generally applicable as a plug-in module for predictive decision-making for arbitrary probabilistic programs, irrespective of the posterior inference strategy. We demonstrate the approach empirically in several problems, confirming its potential.

Variational Bayesian Decision-making for Continuous Utilities

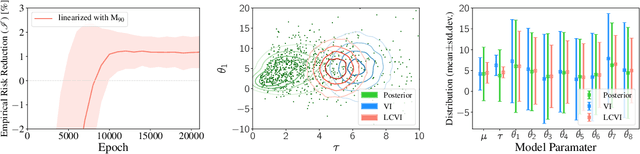
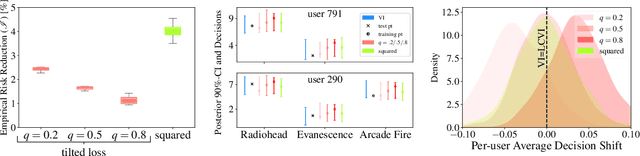
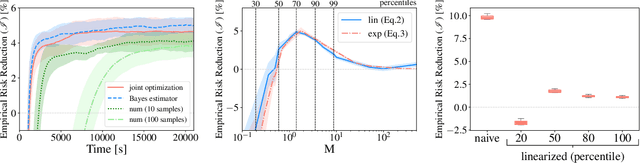
Bayesian decision theory outlines a rigorous framework for making optimal decisions based on maximizing expected utility over a model posterior. However, practitioners often do not have access to the full posterior and resort to approximate inference strategies. In such cases, taking the eventual decision-making task into account while performing the inference allows for calibrating the posterior approximation to maximize the utility. We present an automatic pipeline that co-opts continuous utilities into variational inference algorithms to account for decision-making. We provide practical strategies for approximating and maximizing gain, and empirically demonstrate consistent improvement when calibrating approximations for specific utilities.

Importance Sampled Stochastic Optimization for Variational Inference

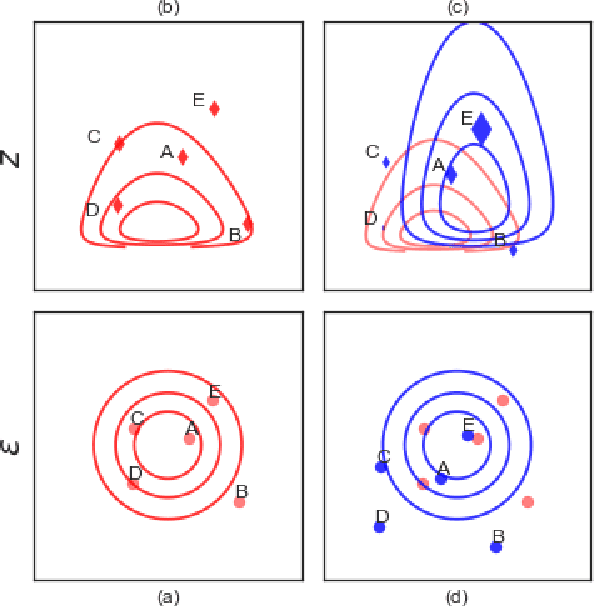
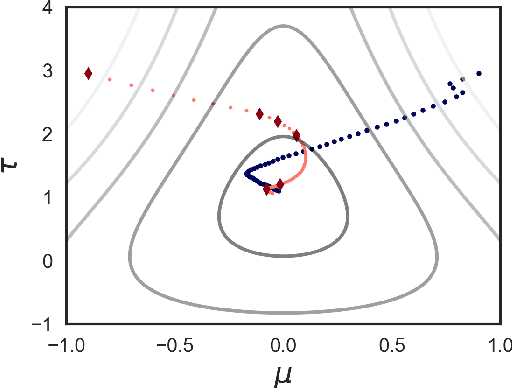
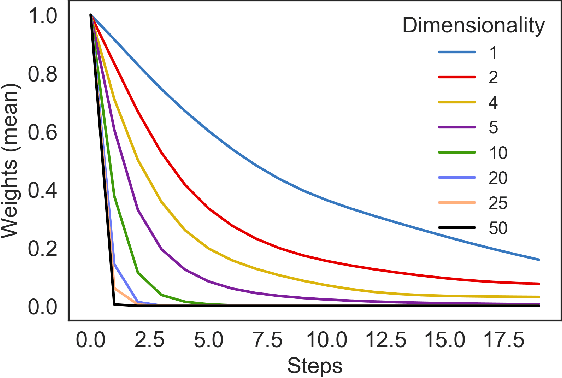
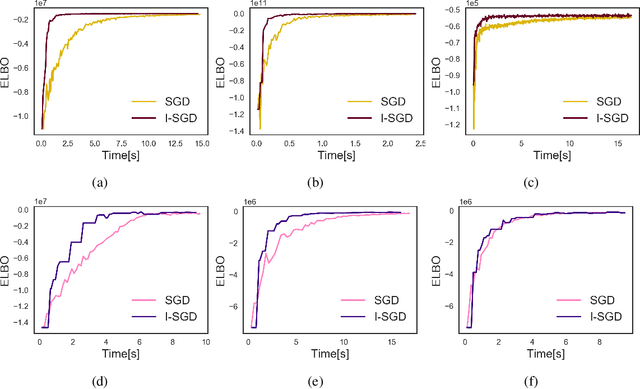
Variational inference approximates the posterior distribution of a probabilistic model with a parameterized density by maximizing a lower bound for the model evidence. Modern solutions fit a flexible approximation with stochastic gradient descent, using Monte Carlo approximation for the gradients. This enables variational inference for arbitrary differentiable probabilistic models, and consequently makes variational inference feasible for probabilistic programming languages. In this work we develop more efficient inference algorithms for the task by considering importance sampling estimates for the gradients. We show how the gradient with respect to the approximation parameters can often be evaluated efficiently without needing to re-compute gradients of the model itself, and then proceed to derive practical algorithms that use importance sampled estimates to speed up computation.We present importance sampled stochastic gradient descent that outperforms standard stochastic gradient descent by a clear margin for a range of models, and provide a justifiable variant of stochastic average gradients for variational inference.