Relative Molecule Self-Attention Transformer

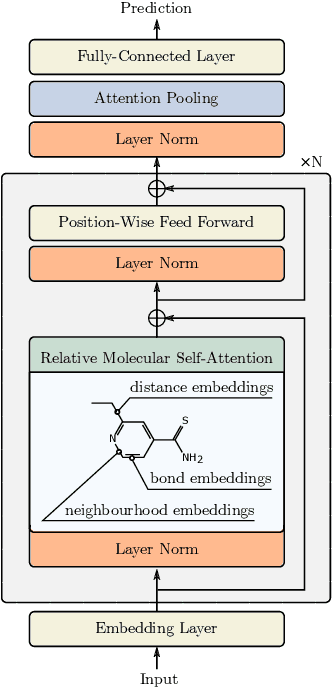
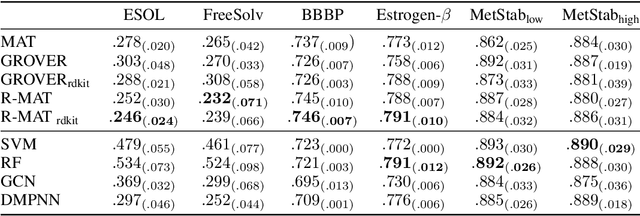
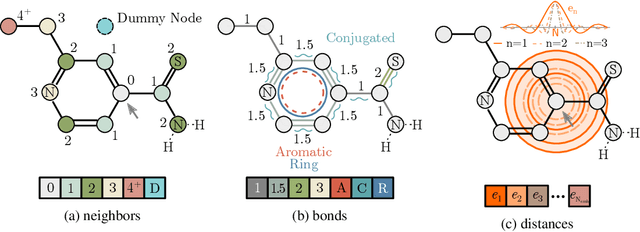
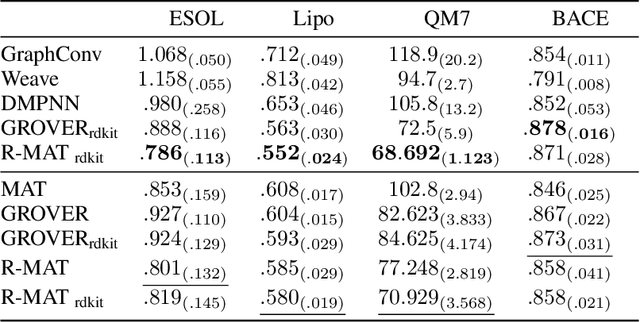
Self-supervised learning holds promise to revolutionize molecule property prediction - a central task to drug discovery and many more industries - by enabling data efficient learning from scarce experimental data. Despite significant progress, non-pretrained methods can be still competitive in certain settings. We reason that architecture might be a key bottleneck. In particular, enriching the backbone architecture with domain-specific inductive biases has been key for the success of self-supervised learning in other domains. In this spirit, we methodologically explore the design space of the self-attention mechanism tailored to molecular data. We identify a novel variant of self-attention adapted to processing molecules, inspired by the relative self-attention layer, which involves fusing embedded graph and distance relationships between atoms. Our main contribution is Relative Molecule Attention Transformer (R-MAT): a novel Transformer-based model based on the developed self-attention layer that achieves state-of-the-art or very competitive results across a~wide range of molecule property prediction tasks.

Zero Time Waste: Recycling Predictions in Early Exit Neural Networks

The problem of reducing processing time of large deep learning models is a fundamental challenge in many real-world applications. Early exit methods strive towards this goal by attaching additional Internal Classifiers (ICs) to intermediate layers of a neural network. ICs can quickly return predictions for easy examples and, as a result, reduce the average inference time of the whole model. However, if a particular IC does not decide to return an answer early, its predictions are discarded, with its computations effectively being wasted. To solve this issue, we introduce Zero Time Waste (ZTW), a novel approach in which each IC reuses predictions returned by its predecessors by (1) adding direct connections between ICs and (2) combining previous outputs in an ensemble-like manner. We conduct extensive experiments across various datasets and architectures to demonstrate that ZTW achieves a significantly better accuracy vs. inference time trade-off than other recently proposed early exit methods.

Generative models with kernel distance in data space

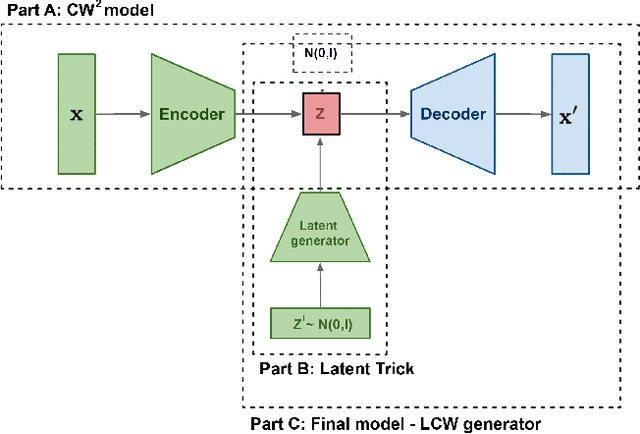
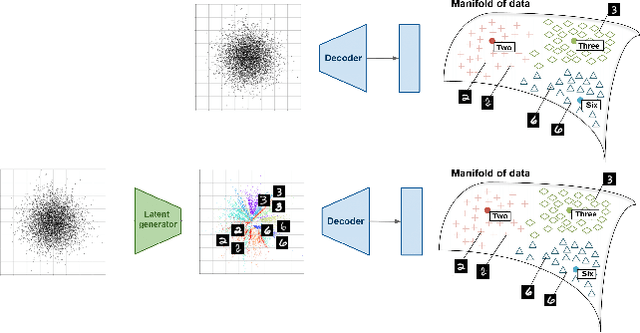
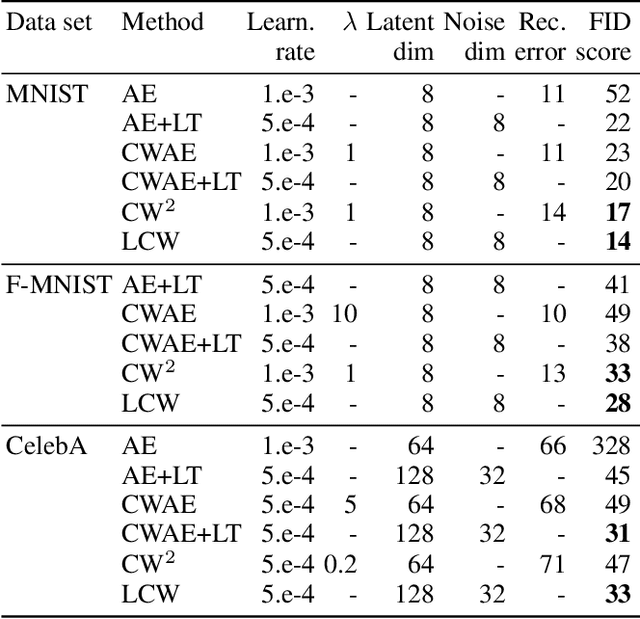
Generative models dealing with modeling a~joint data distribution are generally either autoencoder or GAN based. Both have their pros and cons, generating blurry images or being unstable in training or prone to mode collapse phenomenon, respectively. The objective of this paper is to construct a~model situated between above architectures, one that does not inherit their main weaknesses. The proposed LCW generator (Latent Cramer-Wold generator) resembles a classical GAN in transforming Gaussian noise into data space. What is of utmost importance, instead of a~discriminator, LCW generator uses kernel distance. No adversarial training is utilized, hence the name generator. It is trained in two phases. First, an autoencoder based architecture, using kernel measures, is built to model a manifold of data. We propose a Latent Trick mapping a Gaussian to latent in order to get the final model. This results in very competitive FID values.

One-element Batch Training by Moving Window

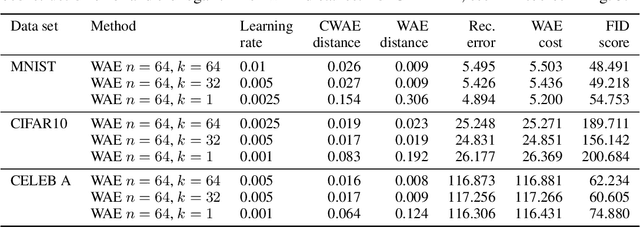
Several deep models, esp. the generative, compare the samples from two distributions (e.g. WAE like AutoEncoder models, set-processing deep networks, etc) in their cost functions. Using all these methods one cannot train the model directly taking small size (in extreme -- one element) batches, due to the fact that samples are to be compared. We propose a generic approach to training such models using one-element mini-batches. The idea is based on splitting the batch in latent into parts: previous, i.e. historical, elements used for latent space distribution matching and the current ones, used both for latent distribution computation and the minimization process. Due to the smaller memory requirements, this allows to train networks on higher resolution images then in the classical approach.

Interpolation in generative models

We show how to construct smooth and realistic interpolations for generative models, with arbitrary, not necessarily Gaussian, prior. The crucial idea is based on the construction on the realisticity index of a curve, which maximisation, as we show, leads to a search of a geodesic with respect to the corresponding Riemann structure.

Sliced generative models

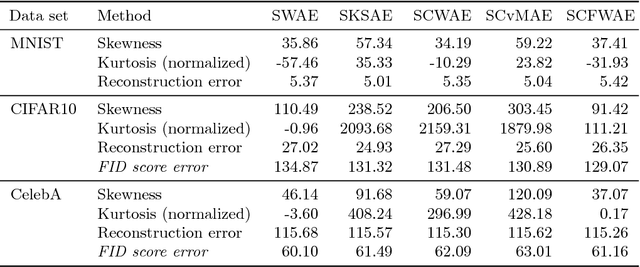
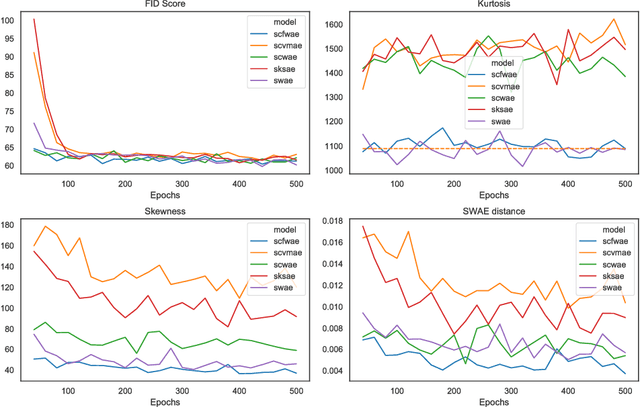
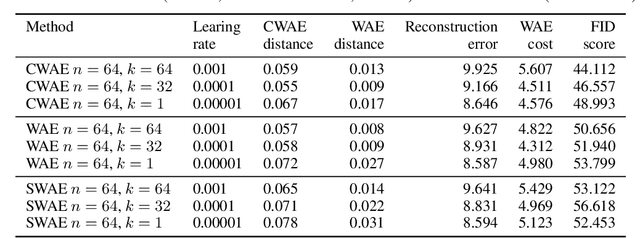
In this paper we discuss a class of AutoEncoder based generative models based on one dimensional sliced approach. The idea is based on the reduction of the discrimination between samples to one-dimensional case. Our experiments show that methods can be divided into two groups. First consists of methods which are a modification of standard normality tests, while the second is based on classical distances between samples. It turns out that both groups are correct generative models, but the second one gives a slightly faster decrease rate of Fr\'{e}chet Inception Distance (FID).

Cramer-Wold AutoEncoder

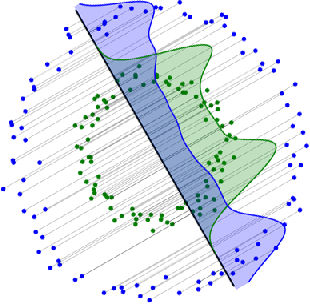
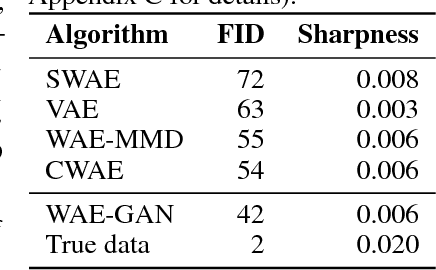
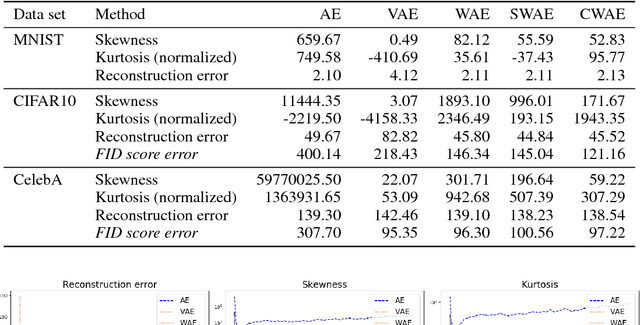
We propose a new generative model, Cramer-Wold Autoencoder (CWAE). Following WAE, we directly encourage normality of the latent space. Our paper uses also the recent idea from Sliced WAE (SWAE) model, which uses one-dimensional projections as a method of verifying closeness of two distributions. The crucial new ingredient is the introduction of a new (Cramer-Wold) metric in the space of densities, which replaces the Wasserstein metric used in SWAE. We show that the Cramer-Wold metric between Gaussian mixtures is given by a simple analytic formula, which results in the removal of sampling necessary to estimate the cost function in WAE and SWAE models. As a consequence, while drastically simplifying the optimization procedure, CWAE produces samples of a matching perceptual quality to other SOTA models.

On Latent Distributions Without Finite Mean in Generative Models

We investigate the properties of multidimensional probability distributions in the context of latent space prior distributions of implicit generative models. Our work revolves around the phenomena arising while decoding linear interpolations between two random latent vectors -- regions of latent space in close proximity to the origin of the space are sampled causing distribution mismatch. We show that due to the Central Limit Theorem, this region is almost never sampled during the training process. As a result, linear interpolations may generate unrealistic data and their usage as a tool to check quality of the trained model is questionable. We propose to use multidimensional Cauchy distribution as the latent prior. Cauchy distribution does not satisfy the assumptions of the CLT and has a number of properties that allow it to work well in conjunction with linear interpolations. We also provide two general methods of creating non-linear interpolations that are easily applicable to a large family of common latent distributions. Finally we empirically analyze the quality of data generated from low-probability-mass regions for the DCGAN model on the CelebA dataset.