Tiered Pruning for Efficient Differentialble Inference-Aware Neural Architecture Search

We propose three novel pruning techniques to improve the cost and results of inference-aware Differentiable Neural Architecture Search (DNAS). First, we introduce , a stochastic bi-path building block for DNAS, which can search over inner hidden dimensions with memory and compute complexity. Second, we present an algorithm for pruning blocks within a stochastic layer of the SuperNet during the search. Third, we describe a novel technique for pruning unnecessary stochastic layers during the search. The optimized models resulting from the search are called PruNet and establishes a new state-of-the-art Pareto frontier for NVIDIA V100 in terms of inference latency for ImageNet Top-1 image classification accuracy. PruNet as a backbone also outperforms GPUNet and EfficientNet on the COCO object detection task on inference latency relative to mean Average Precision (mAP).

Relative Molecule Self-Attention Transformer

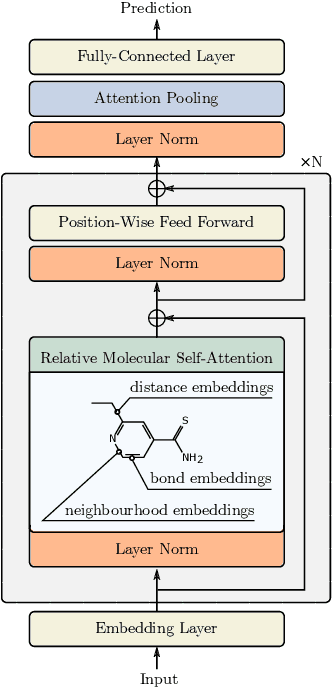
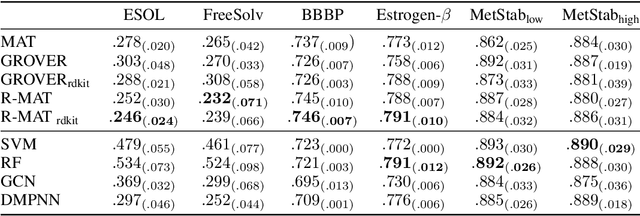
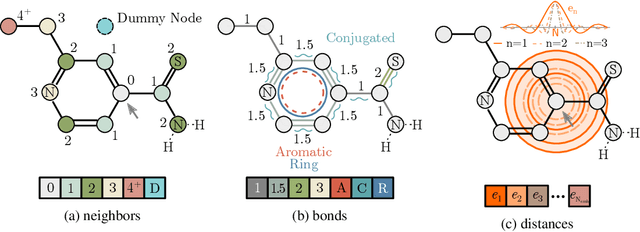
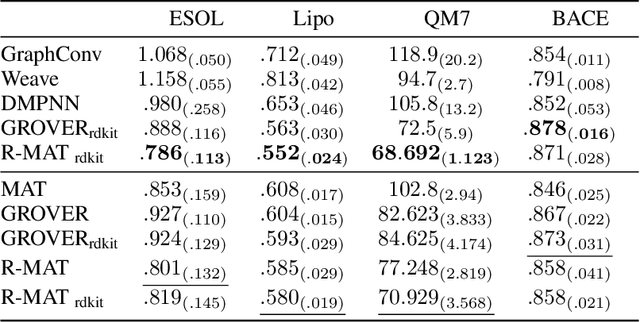
Self-supervised learning holds promise to revolutionize molecule property prediction - a central task to drug discovery and many more industries - by enabling data efficient learning from scarce experimental data. Despite significant progress, non-pretrained methods can be still competitive in certain settings. We reason that architecture might be a key bottleneck. In particular, enriching the backbone architecture with domain-specific inductive biases has been key for the success of self-supervised learning in other domains. In this spirit, we methodologically explore the design space of the self-attention mechanism tailored to molecular data. We identify a novel variant of self-attention adapted to processing molecules, inspired by the relative self-attention layer, which involves fusing embedded graph and distance relationships between atoms. Our main contribution is Relative Molecule Attention Transformer (R-MAT): a novel Transformer-based model based on the developed self-attention layer that achieves state-of-the-art or very competitive results across a~wide range of molecule property prediction tasks.

Efficient GPU implementation of randomized SVD and its applications

Matrix decompositions are ubiquitous in machine learning, including applications in dimensionality reduction, data compression and deep learning algorithms. Typical solutions for matrix decompositions have polynomial complexity which significantly increases their computational cost and time. In this work, we leverage efficient processing operations that can be run in parallel on modern Graphical Processing Units (GPUs), predominant computing architecture used e.g. in deep learning, to reduce the computational burden of computing matrix decompositions. More specifically, we reformulate the randomized decomposition problem to incorporate fast matrix multiplication operations (BLAS-3) as building blocks. We show that this formulation, combined with fast random number generators, allows to fully exploit the potential of parallel processing implemented in GPUs. Our extensive evaluation confirms the superiority of this approach over the competing methods and we release the results of this research as a part of the official CUDA implementation (https://docs.nvidia.com/cuda/cusolver/index.html).