Cramer-Wold AutoEncoder
Paper and Code
Oct 04, 2018
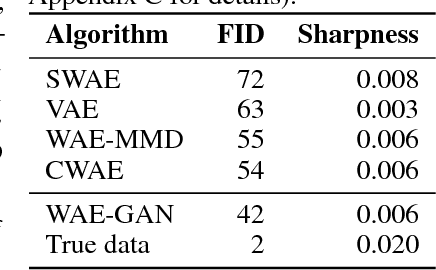

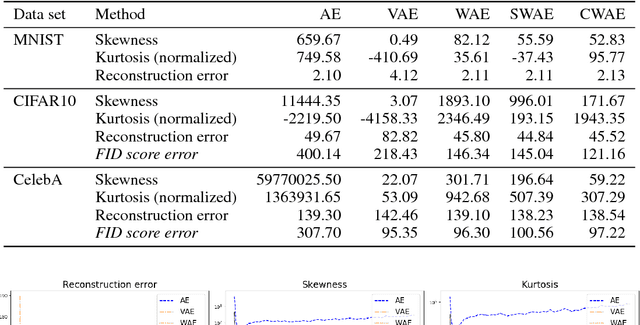
We propose a new generative model, Cramer-Wold Autoencoder (CWAE). Following WAE, we directly encourage normality of the latent space. Our paper uses also the recent idea from Sliced WAE (SWAE) model, which uses one-dimensional projections as a method of verifying closeness of two distributions. The crucial new ingredient is the introduction of a new (Cramer-Wold) metric in the space of densities, which replaces the Wasserstein metric used in SWAE. We show that the Cramer-Wold metric between Gaussian mixtures is given by a simple analytic formula, which results in the removal of sampling necessary to estimate the cost function in WAE and SWAE models. As a consequence, while drastically simplifying the optimization procedure, CWAE produces samples of a matching perceptual quality to other SOTA models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge