CCuantuMM: Cycle-Consistent Quantum-Hybrid Matching of Multiple Shapes

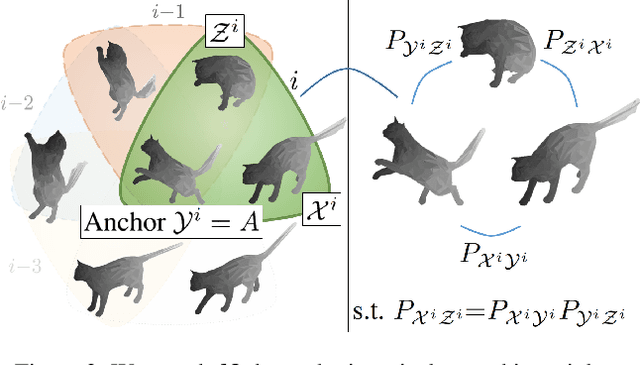
Jointly matching multiple, non-rigidly deformed 3D shapes is a challenging, $\mathcal{NP}$-hard problem. A perfect matching is necessarily cycle-consistent: Following the pairwise point correspondences along several shapes must end up at the starting vertex of the original shape. Unfortunately, existing quantum shape-matching methods do not support multiple shapes and even less cycle consistency. This paper addresses the open challenges and introduces the first quantum-hybrid approach for 3D shape multi-matching; in addition, it is also cycle-consistent. Its iterative formulation is admissible to modern adiabatic quantum hardware and scales linearly with the total number of input shapes. Both these characteristics are achieved by reducing the $N$-shape case to a sequence of three-shape matchings, the derivation of which is our main technical contribution. Thanks to quantum annealing, high-quality solutions with low energy are retrieved for the intermediate $\mathcal{NP}$-hard objectives. On benchmark datasets, the proposed approach significantly outperforms extensions to multi-shape matching of a previous quantum-hybrid two-shape matching method and is on-par with classical multi-matching methods.

QuAnt: Quantum Annealing with Learnt Couplings

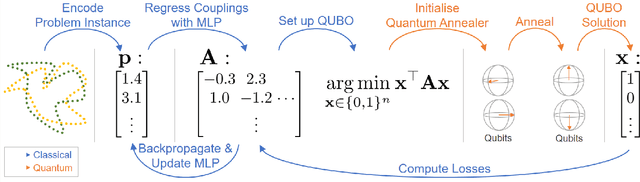
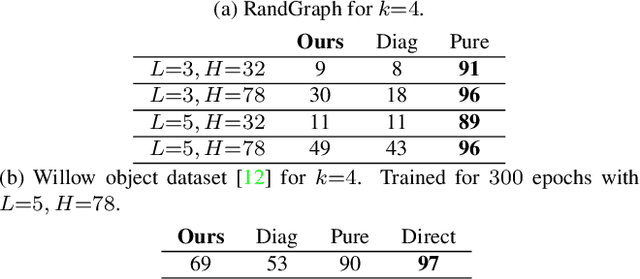
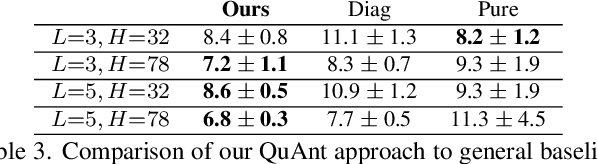
Modern quantum annealers can find high-quality solutions to combinatorial optimisation objectives given as quadratic unconstrained binary optimisation (QUBO) problems. Unfortunately, obtaining suitable QUBO forms in computer vision remains challenging and currently requires problem-specific analytical derivations. Moreover, such explicit formulations impose tangible constraints on solution encodings. In stark contrast to prior work, this paper proposes to learn QUBO forms from data through gradient backpropagation instead of deriving them. As a result, the solution encodings can be chosen flexibly and compactly. Furthermore, our methodology is general and virtually independent of the specifics of the target problem type. We demonstrate the advantages of learnt QUBOs on the diverse problem types of graph matching, 2D point cloud alignment and 3D rotation estimation. Our results are competitive with the previous quantum state of the art while requiring much fewer logical and physical qubits, enabling our method to scale to larger problems. The code and the new dataset will be open-sourced.

Quantum Motion Segmentation

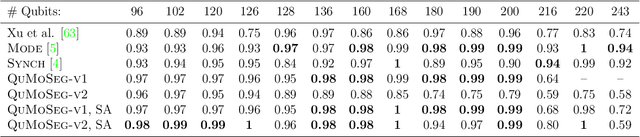
Motion segmentation is a challenging problem that seeks to identify independent motions in two or several input images. This paper introduces the first algorithm for motion segmentation that relies on adiabatic quantum optimization of the objective function. The proposed method achieves on-par performance with the state of the art on problem instances which can be mapped to modern quantum annealers.

Adiabatic Quantum Graph Matching with Permutation Matrix Constraints

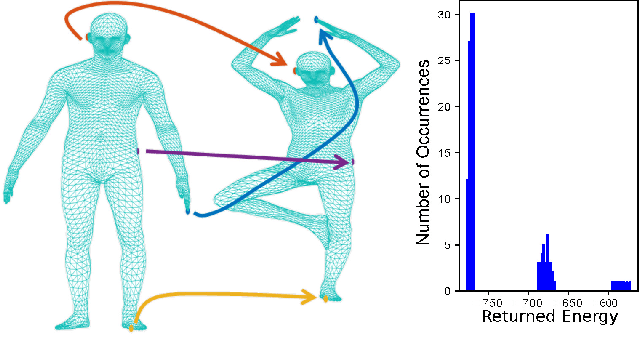
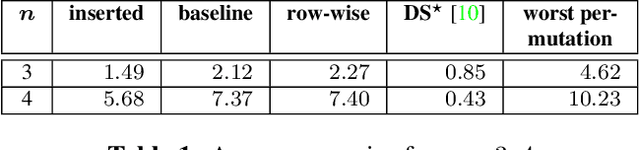
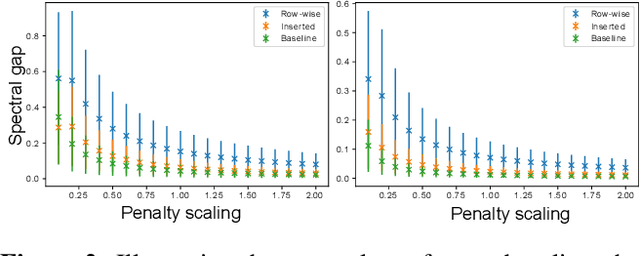
Matching problems on 3D shapes and images are challenging as they are frequently formulated as combinatorial quadratic assignment problems (QAPs) with permutation matrix constraints, which are NP-hard. In this work, we address such problems with emerging quantum computing technology and propose several reformulations of QAPs as unconstrained problems suitable for efficient execution on quantum hardware. We investigate several ways to inject permutation matrix constraints in a quadratic unconstrained binary optimization problem which can be mapped to quantum hardware. We focus on obtaining a sufficient spectral gap, which further increases the probability to measure optimal solutions and valid permutation matrices in a single run. We perform our experiments on the quantum computer D-Wave 2000Q (2^11 qubits, adiabatic). Despite the observed discrepancy between simulated adiabatic quantum computing and execution on real quantum hardware, our reformulation of permutation matrix constraints increases the robustness of the numerical computations over other penalty approaches in our experiments. The proposed algorithm has the potential to scale to higher dimensions on future quantum computing architectures, which opens up multiple new directions for solving matching problems in 3D computer vision and graphics.

Q-Match: Iterative Shape Matching via Quantum Annealing

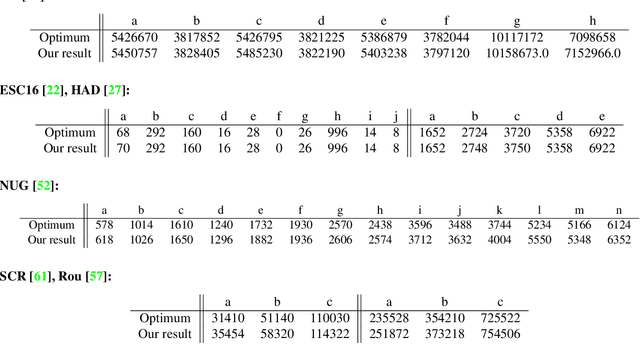
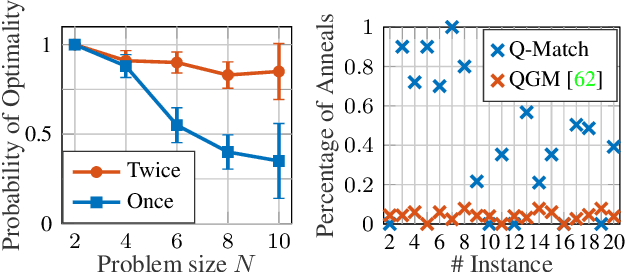
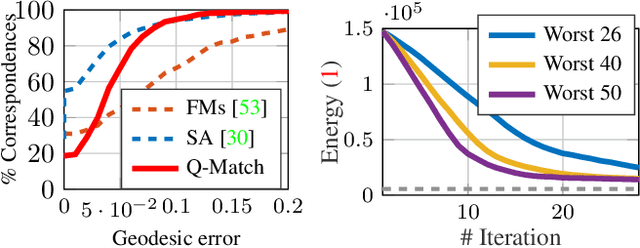
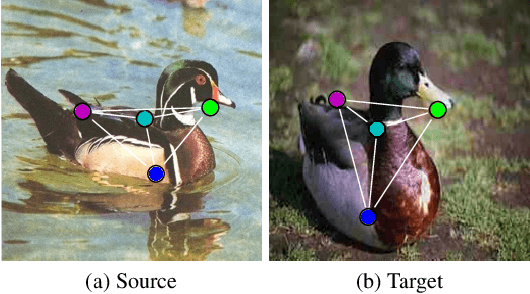
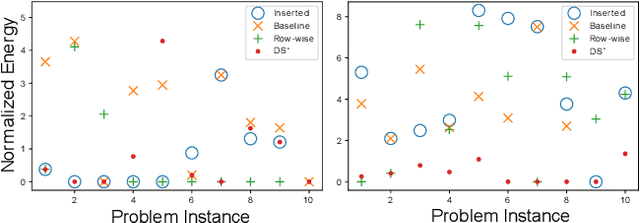
Finding shape correspondences can be formulated as an NP-hard quadratic assignment problem (QAP) that becomes infeasible for shapes with high sampling density. A promising research direction is to tackle such quadratic optimization problems over binary variables with quantum annealing, which, in theory, allows to find globally optimal solutions relying on a new computational paradigm. Unfortunately, enforcing the linear equality constraints in QAPs via a penalty significantly limits the success probability of such methods on currently available quantum hardware. To address this limitation, this paper proposes Q-Match, i.e., a new iterative quantum method for QAPs inspired by the alpha-expansion algorithm, which allows solving problems of an order of magnitude larger than current quantum methods. It works by implicitly enforcing the QAP constraints by updating the current estimates in a cyclic fashion. Further, Q-Match can be applied for shape matching problems iteratively, on a subset of well-chosen correspondences, allowing us to scale to real-world problems. Using the latest quantum annealer, the D-Wave Advantage, we evaluate the proposed method on a subset of QAPLIB as well as on isometric shape matching problems from the FAUST dataset.