CCuantuMM: Cycle-Consistent Quantum-Hybrid Matching of Multiple Shapes
Paper and Code
Mar 28, 2023

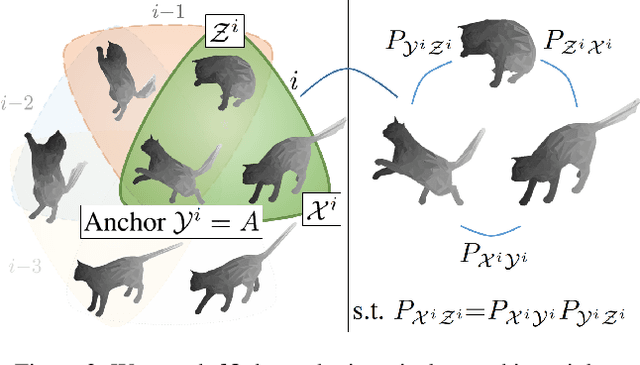

Jointly matching multiple, non-rigidly deformed 3D shapes is a challenging, $\mathcal{NP}$-hard problem. A perfect matching is necessarily cycle-consistent: Following the pairwise point correspondences along several shapes must end up at the starting vertex of the original shape. Unfortunately, existing quantum shape-matching methods do not support multiple shapes and even less cycle consistency. This paper addresses the open challenges and introduces the first quantum-hybrid approach for 3D shape multi-matching; in addition, it is also cycle-consistent. Its iterative formulation is admissible to modern adiabatic quantum hardware and scales linearly with the total number of input shapes. Both these characteristics are achieved by reducing the $N$-shape case to a sequence of three-shape matchings, the derivation of which is our main technical contribution. Thanks to quantum annealing, high-quality solutions with low energy are retrieved for the intermediate $\mathcal{NP}$-hard objectives. On benchmark datasets, the proposed approach significantly outperforms extensions to multi-shape matching of a previous quantum-hybrid two-shape matching method and is on-par with classical multi-matching methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge