Heat Kernel Goes Topological

Topological neural networks have emerged as powerful successors of graph neural networks. However, they typically involve higher-order message passing, which incurs significant computational expense. We circumvent this issue with a novel topological framework that introduces a Laplacian operator on combinatorial complexes (CCs), enabling efficient computation of heat kernels that serve as node descriptors. Our approach captures multiscale information and enables permutation-equivariant representations, allowing easy integration into modern transformer-based architectures. Theoretically, the proposed method is maximally expressive because it can distinguish arbitrary non-isomorphic CCs. Empirically, it significantly outperforms existing topological methods in terms of computational efficiency. Besides demonstrating competitive performance with the state-of-the-art descriptors on standard molecular datasets, it exhibits superior capability in distinguishing complex topological structures and avoiding blind spots on topological benchmarks. Overall, this work advances topological deep learning by providing expressive yet scalable representations, thereby opening up exciting avenues for molecular classification and property prediction tasks.

Projected Stochastic Gradient Descent with Quantum Annealed Binary Gradients

We present, QP-SBGD, a novel layer-wise stochastic optimiser tailored towards training neural networks with binary weights, known as binary neural networks (BNNs), on quantum hardware. BNNs reduce the computational requirements and energy consumption of deep learning models with minimal loss in accuracy. However, training them in practice remains to be an open challenge. Most known BNN-optimisers either rely on projected updates or binarise weights post-training. Instead, QP-SBGD approximately maps the gradient onto binary variables, by solving a quadratic constrained binary optimisation. Under practically reasonable assumptions, we show that this update rule converges with a rate of $\mathcal{O}(1 / \sqrt{T})$. Moreover, we show how the $\mathcal{NP}$-hard projection can be effectively executed on an adiabatic quantum annealer, harnessing recent advancements in quantum computation. We also introduce a projected version of this update rule and prove that if a fixed point exists in the binary variable space, the modified updates will converge to it. Last but not least, our algorithm is implemented layer-wise, making it suitable to train larger networks on resource-limited quantum hardware. Through extensive evaluations, we show that QP-SBGD outperforms or is on par with competitive and well-established baselines such as BinaryConnect, signSGD and ProxQuant when optimising the Rosenbrock function, training BNNs as well as binary graph neural networks.

TIDE: Time Derivative Diffusion for Deep Learning on Graphs

A prominent paradigm for graph neural networks is based on the message passing framework. In this framework, information communication is realized only between neighboring nodes. The challenge of approaches that use this paradigm is to ensure efficient and accurate \textit{long distance communication} between nodes, as deep convolutional networks are prone to over-smoothing. In this paper, we present a novel method based on time derivative graph diffusion (TIDE), with a learnable time parameter. Our approach allows to adapt the spatial extent of diffusion across different tasks and network channels, thus enabling medium and long-distance communication efficiently. Furthermore, we show that our architecture directly enables local message passing and thus inherits from the expressive power of local message passing approaches. We show that on widely used graph benchmarks we achieve comparable performance and on a synthetic mesh dataset we outperform state-of-the-art methods like GCN or GRAND by a significant margin.

QuAnt: Quantum Annealing with Learnt Couplings

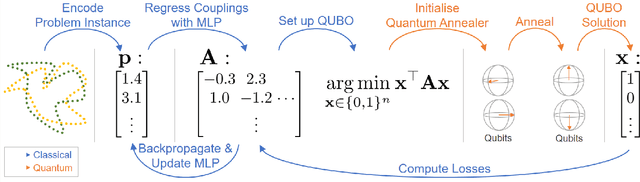
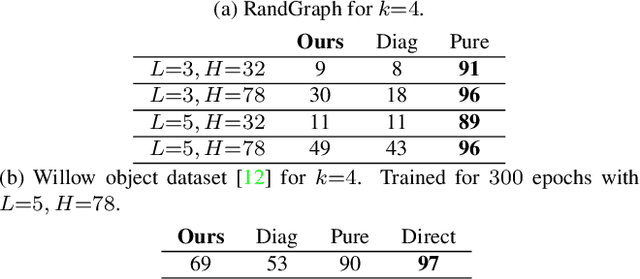
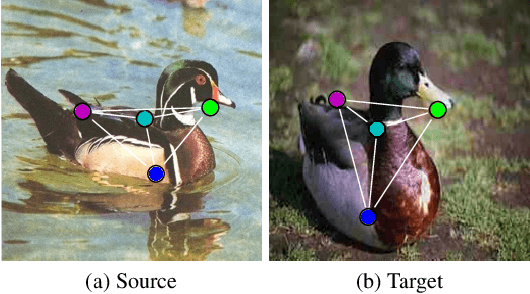
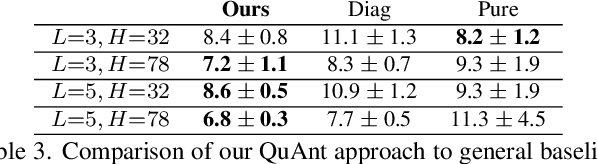
Modern quantum annealers can find high-quality solutions to combinatorial optimisation objectives given as quadratic unconstrained binary optimisation (QUBO) problems. Unfortunately, obtaining suitable QUBO forms in computer vision remains challenging and currently requires problem-specific analytical derivations. Moreover, such explicit formulations impose tangible constraints on solution encodings. In stark contrast to prior work, this paper proposes to learn QUBO forms from data through gradient backpropagation instead of deriving them. As a result, the solution encodings can be chosen flexibly and compactly. Furthermore, our methodology is general and virtually independent of the specifics of the target problem type. We demonstrate the advantages of learnt QUBOs on the diverse problem types of graph matching, 2D point cloud alignment and 3D rotation estimation. Our results are competitive with the previous quantum state of the art while requiring much fewer logical and physical qubits, enabling our method to scale to larger problems. The code and the new dataset will be open-sourced.

Convex Joint Graph Matching and Clustering via Semidefinite Relaxations

This paper proposes a new algorithm for simultaneous graph matching and clustering. For the first time in the literature, these two problems are solved jointly and synergetically without relying on any training data, which brings advantages for identifying similar arbitrary objects in compound 3D scenes and matching them. For joint reasoning, we first rephrase graph matching as a rigid point set registration problem operating on spectral graph embeddings. Consequently, we utilise efficient convex semidefinite program relaxations for aligning points in Hilbert spaces and add coupling constraints to model the mutual dependency and exploit synergies between both tasks. We outperform state of the art in challenging cases with non-perfectly matching and noisy graphs, and we show successful applications on real compound scenes with multiple 3D elements. Our source code and data are publicly available.