Smoothed Graph Contrastive Learning via Seamless Proximity Integration

Graph contrastive learning (GCL) aligns node representations by classifying node pairs into positives and negatives using a selection process that typically relies on establishing correspondences within two augmented graphs. The conventional GCL approaches incorporate negative samples uniformly in the contrastive loss, resulting in the equal treatment negative nodes, regardless of their proximity to the true positive. In this paper, we present a Smoothed Graph Contrastive Learning model (SGCL), which leverages the geometric structure of augmented graphs to inject proximity information associated with positive/negative pairs in the contrastive loss, thus significantly regularizing the learning process. The proposed SGCL adjusts the penalties associated with node pairs in the contrastive loss by incorporating three distinct smoothing techniques that result in proximity aware positives and negatives. To enhance scalability for large-scale graphs, the proposed framework incorporates a graph batch-generating strategy that partitions the given graphs into multiple subgraphs, facilitating efficient training in separate batches. Through extensive experimentation in the unsupervised setting on various benchmarks, particularly those of large scale, we demonstrate the superiority of our proposed framework against recent baselines.

TIDE: Time Derivative Diffusion for Deep Learning on Graphs

A prominent paradigm for graph neural networks is based on the message passing framework. In this framework, information communication is realized only between neighboring nodes. The challenge of approaches that use this paradigm is to ensure efficient and accurate \textit{long distance communication} between nodes, as deep convolutional networks are prone to over-smoothing. In this paper, we present a novel method based on time derivative graph diffusion (TIDE), with a learnable time parameter. Our approach allows to adapt the spatial extent of diffusion across different tasks and network channels, thus enabling medium and long-distance communication efficiently. Furthermore, we show that our architecture directly enables local message passing and thus inherits from the expressive power of local message passing approaches. We show that on widely used graph benchmarks we achieve comparable performance and on a synthetic mesh dataset we outperform state-of-the-art methods like GCN or GRAND by a significant margin.

Geometric Multimodal Deep Learning with Multi-Scaled Graph Wavelet Convolutional Network

Multimodal data provide complementary information of a natural phenomenon by integrating data from various domains with very different statistical properties. Capturing the intra-modality and cross-modality information of multimodal data is the essential capability of multimodal learning methods. The geometry-aware data analysis approaches provide these capabilities by implicitly representing data in various modalities based on their geometric underlying structures. Also, in many applications, data are explicitly defined on an intrinsic geometric structure. Generalizing deep learning methods to the non-Euclidean domains is an emerging research field, which has recently been investigated in many studies. Most of those popular methods are developed for unimodal data. In this paper, a multimodal multi-scaled graph wavelet convolutional network (M-GWCN) is proposed as an end-to-end network. M-GWCN simultaneously finds intra-modality representation by applying the multiscale graph wavelet transform to provide helpful localization properties in the graph domain of each modality, and cross-modality representation by learning permutations that encode correlations among various modalities. M-GWCN is not limited to either the homogeneous modalities with the same number of data, or any prior knowledge indicating correspondences between modalities. Several semi-supervised node classification experiments have been conducted on three popular unimodal explicit graph-based datasets and five multimodal implicit ones. The experimental results indicate the superiority and effectiveness of the proposed methods compared with both spectral graph domain convolutional neural networks and state-of-the-art multimodal methods.

Weighted Least Squares Twin Support Vector Machine with Fuzzy Rough Set Theory for Imbalanced Data Classification

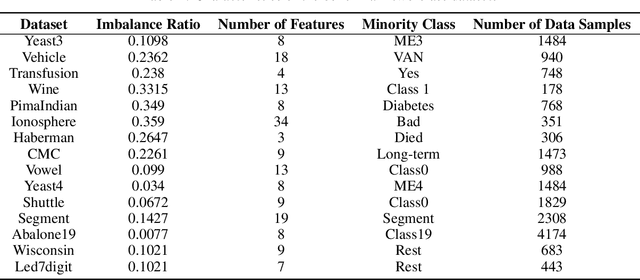
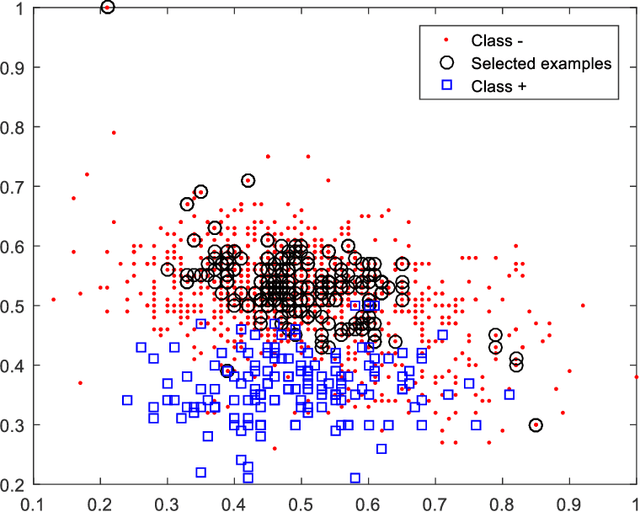
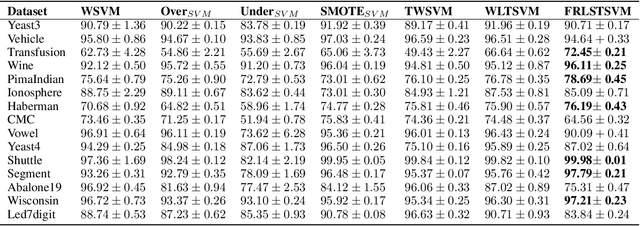
Support vector machines (SVMs) are powerful supervised learning tools developed to solve classification problems. However, SVMs are likely to perform poorly in the classification of imbalanced data. The rough set theory presents a mathematical tool for inference in nondeterministic cases that provides methods for removing irrelevant information from data. In this work, we propose an approach that efficiently used fuzzy rough set theory in weighted least squares twin support vector machine called FRLSTSVM for classification of imbalanced data. The first innovation is introducing a new fuzzy rough set-based under-sampling strategy to make the classifier robust in terms of the imbalanced data. For constructing the two proximal hyperplanes in FRLSTSVM, data points from the minority class remain unchanged while a subset of data points in the majority class are selected using a new method. In this model, we embed the weight biases in the LSTSVM formulations to overcome the bias phenomenon in the original twin SVM for the classification of imbalanced data. In order to determine these weights in this formulation, we introduce a new strategy that uses fuzzy rough set theory as the second innovation. Experimental results on the famous imbalanced datasets, compared to the related traditional SVM-based methods, demonstrate the superiority of the proposed FRLSTSVM model in the imbalanced data classification.

Cross-Modal and Multimodal Data Analysis Based on Functional Mapping of Spectral Descriptors and Manifold Regularization

Multimodal manifold modeling methods extend the spectral geometry-aware data analysis to learning from several related and complementary modalities. Most of these methods work based on two major assumptions: 1) there are the same number of homogeneous data samples in each modality, and 2) at least partial correspondences between modalities are given in advance as prior knowledge. This work proposes two new multimodal modeling methods. The first method establishes a general analyzing framework to deal with the multimodal information problem for heterogeneous data without any specific prior knowledge. For this purpose, first, we identify the localities of each manifold by extracting local descriptors via spectral graph wavelet signatures (SGWS). Then, we propose a manifold regularization framework based on the functional mapping between SGWS descriptors (FMBSD) for finding the pointwise correspondences. The second method is a manifold regularized multimodal classification based on pointwise correspondences (M$^2$CPC) used for the problem of multiclass classification of multimodal heterogeneous, which the correspondences between modalities are determined based on the FMBSD method. The experimental results of evaluating the FMBSD method on three common cross-modal retrieval datasets and evaluating the (M$^2$CPC) method on three benchmark multimodal multiclass classification datasets indicate their effectiveness and superiority over state-of-the-art methods.