Kissing to Find a Match: Efficient Low-Rank Permutation Representation

Permutation matrices play a key role in matching and assignment problems across the fields, especially in computer vision and robotics. However, memory for explicitly representing permutation matrices grows quadratically with the size of the problem, prohibiting large problem instances. In this work, we propose to tackle the curse of dimensionality of large permutation matrices by approximating them using low-rank matrix factorization, followed by a nonlinearity. To this end, we rely on the Kissing number theory to infer the minimal rank required for representing a permutation matrix of a given size, which is significantly smaller than the problem size. This leads to a drastic reduction in computation and memory costs, e.g., up to $3$ orders of magnitude less memory for a problem of size $n=20000$, represented using $8.4\times10^5$ elements in two small matrices instead of using a single huge matrix with $4\times 10^8$ elements. The proposed representation allows for accurate representations of large permutation matrices, which in turn enables handling large problems that would have been infeasible otherwise. We demonstrate the applicability and merits of the proposed approach through a series of experiments on a range of problems that involve predicting permutation matrices, from linear and quadratic assignment to shape matching problems.

Depthwise Separable Convolutions Allow for Fast and Memory-Efficient Spectral Normalization

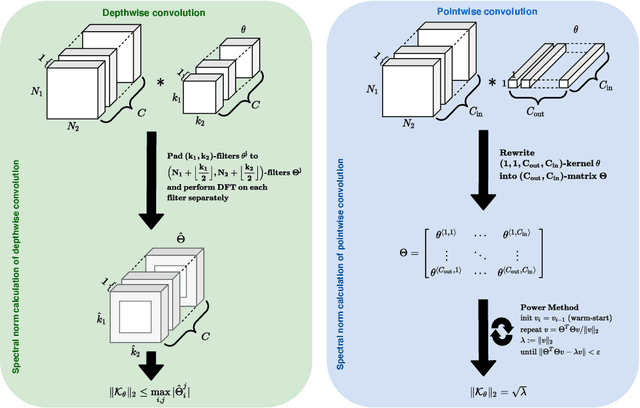
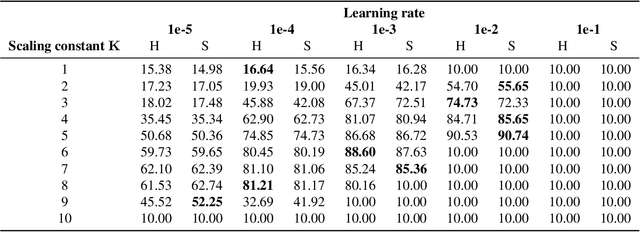
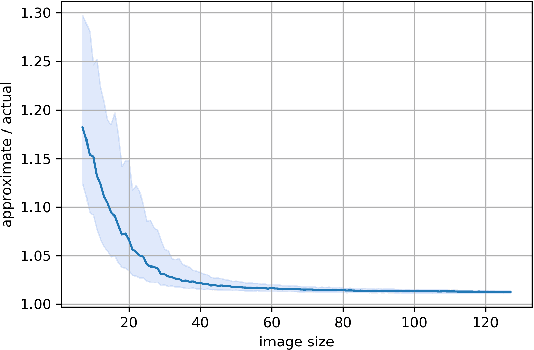
An increasing number of models require the control of the spectral norm of convolutional layers of a neural network. While there is an abundance of methods for estimating and enforcing upper bounds on those during training, they are typically costly in either memory or time. In this work, we introduce a very simple method for spectral normalization of depthwise separable convolutions, which introduces negligible computational and memory overhead. We demonstrate the effectiveness of our method on image classification tasks using standard architectures like MobileNetV2.

Learning to Identify Physical Parameters from Video Using Differentiable Physics

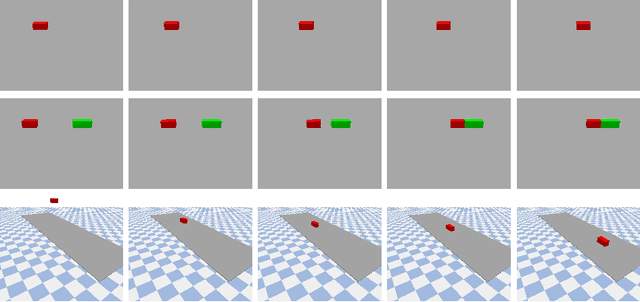
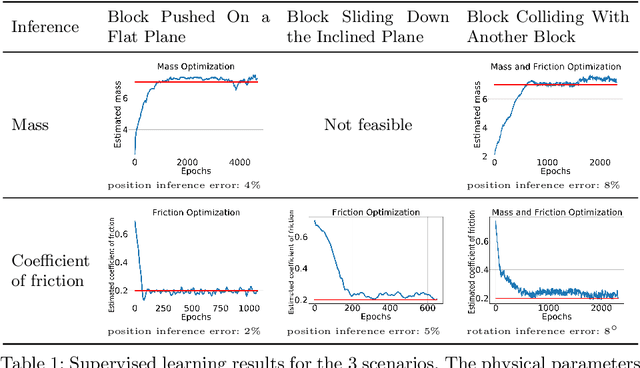
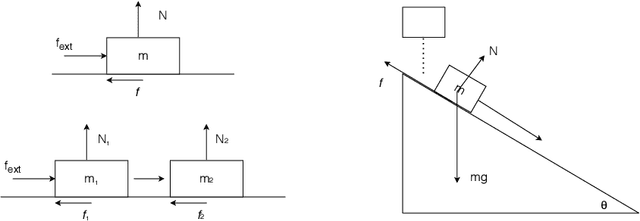
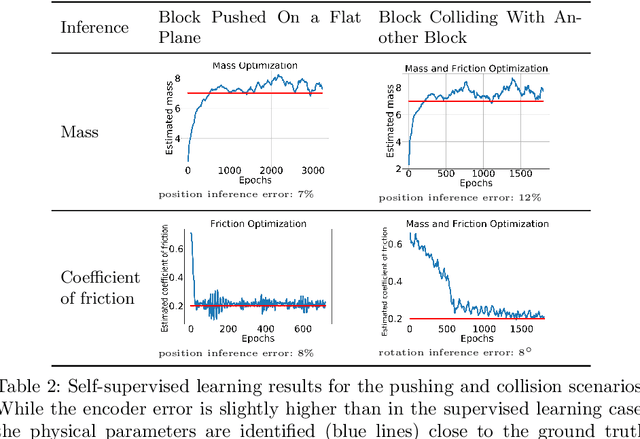
Video representation learning has recently attracted attention in computer vision due to its applications for activity and scene forecasting or vision-based planning and control. Video prediction models often learn a latent representation of video which is encoded from input frames and decoded back into images. Even when conditioned on actions, purely deep learning based architectures typically lack a physically interpretable latent space. In this study, we use a differentiable physics engine within an action-conditional video representation network to learn a physical latent representation. We propose supervised and self-supervised learning methods to train our network and identify physical properties. The latter uses spatial transformers to decode physical states back into images. The simulation scenarios in our experiments comprise pushing, sliding and colliding objects, for which we also analyze the observability of the physical properties. In experiments we demonstrate that our network can learn to encode images and identify physical properties like mass and friction from videos and action sequences in the simulated scenarios. We evaluate the accuracy of our supervised and self-supervised methods and compare it with a system identification baseline which directly learns from state trajectories. We also demonstrate the ability of our method to predict future video frames from input images and actions.

Training Auto-encoder-based Optimizers for Terahertz Image Reconstruction

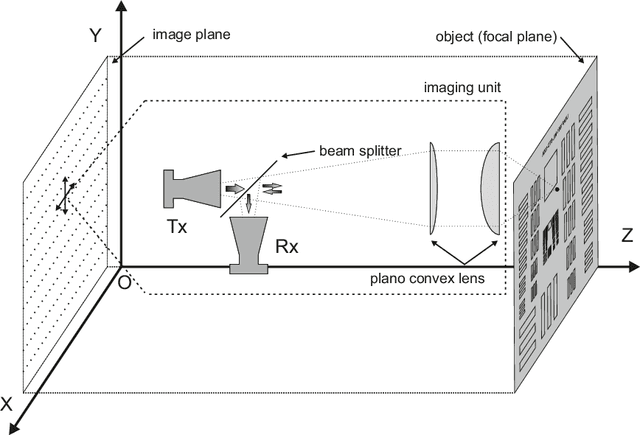
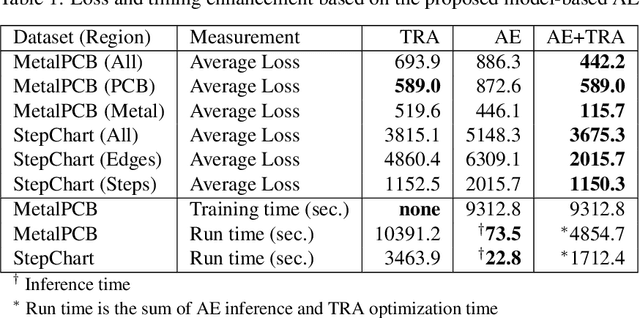
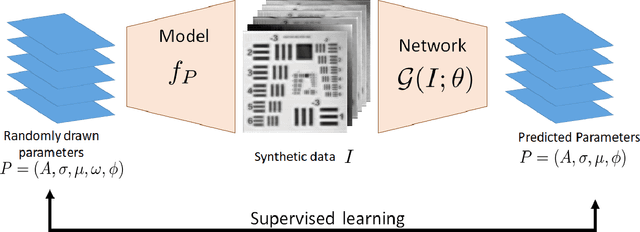
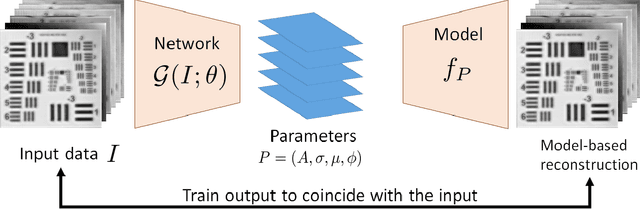
Terahertz (THz) sensing is a promising imaging technology for a wide variety of different applications. Extracting the interpretable and physically meaningful parameters for such applications, however, requires solving an inverse problem in which a model function determined by these parameters needs to be fitted to the measured data. Since the underlying optimization problem is nonconvex and very costly to solve, we propose learning the prediction of suitable parameters from the measured data directly. More precisely, we develop a model-based autoencoder in which the encoder network predicts suitable parameters and the decoder is fixed to a physically meaningful model function, such that we can train the encoding network in an unsupervised way. We illustrate numerically that the resulting network is more than 140 times faster than classical optimization techniques while making predictions with only slightly higher objective values. Using such predictions as starting points of local optimization techniques allows us to converge to better local minima about twice as fast as optimization without the network-based initialization.

Nonlinear Spectral Image Fusion

In this paper we demonstrate that the framework of nonlinear spectral decompositions based on total variation (TV) regularization is very well suited for image fusion as well as more general image manipulation tasks. The well-localized and edge-preserving spectral TV decomposition allows to select frequencies of a certain image to transfer particular features, such as wrinkles in a face, from one image to another. We illustrate the effectiveness of the proposed approach in several numerical experiments, including a comparison to the competing techniques of Poisson image editing, linear osmosis, wavelet fusion and Laplacian pyramid fusion. We conclude that the proposed spectral TV image decomposition framework is a valuable tool for semi- and fully-automatic image editing and fusion.

A convex model for non-negative matrix factorization and dimensionality reduction on physical space

A collaborative convex framework for factoring a data matrix $X$ into a non-negative product $AS$, with a sparse coefficient matrix $S$, is proposed. We restrict the columns of the dictionary matrix $A$ to coincide with certain columns of the data matrix $X$, thereby guaranteeing a physically meaningful dictionary and dimensionality reduction. We use $l_{1,\infty}$ regularization to select the dictionary from the data and show this leads to an exact convex relaxation of $l_0$ in the case of distinct noise free data. We also show how to relax the restriction-to-$X$ constraint by initializing an alternating minimization approach with the solution of the convex model, obtaining a dictionary close to but not necessarily in $X$. We focus on applications of the proposed framework to hyperspectral endmember and abundances identification and also show an application to blind source separation of NMR data.