FUSE: A Flow-based Mapping Between Shapes

We introduce a novel neural representation for maps between 3D shapes based on flow-matching models, which is computationally efficient and supports cross-representation shape matching without large-scale training or data-driven procedures. 3D shapes are represented as the probability distribution induced by a continuous and invertible flow mapping from a fixed anchor distribution. Given a source and a target shape, the composition of the inverse flow (source to anchor) with the forward flow (anchor to target), we continuously map points between the two surfaces. By encoding the shapes with a pointwise task-tailored embedding, this construction provides an invertible and modality-agnostic representation of maps between shapes across point clouds, meshes, signed distance fields (SDFs), and volumetric data. The resulting representation consistently achieves high coverage and accuracy across diverse benchmarks and challenging settings in shape matching. Beyond shape matching, our framework shows promising results in other tasks, including UV mapping and registration of raw point cloud scans of human bodies.

Implicit-ARAP: Efficient Handle-Guided Deformation of High-Resolution Meshes and Neural Fields via Local Patch Meshing

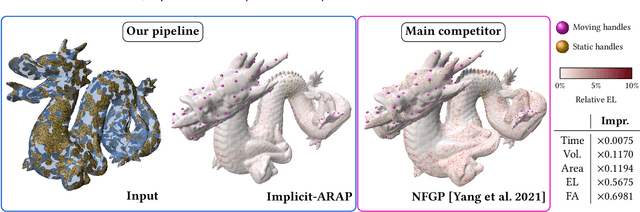
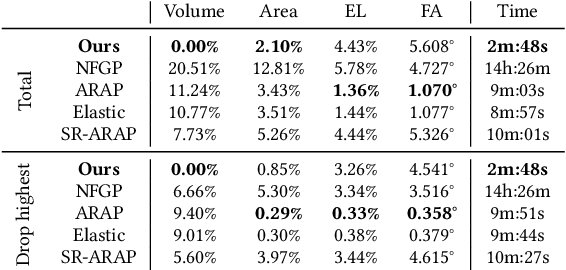
In this work, we present the local patch mesh representation for neural signed distance fields. This technique allows to discretize local regions of the level sets of an input SDF by projecting and deforming flat patch meshes onto the level set surface, using exclusively the SDF information and its gradient. Our analysis reveals this method to be more accurate than the standard marching cubes algorithm for approximating the implicit surface. Then, we apply this representation in the setting of handle-guided deformation: we introduce two distinct pipelines, which make use of 3D neural fields to compute As-Rigid-As-Possible deformations of both high-resolution meshes and neural fields under a given set of constraints. We run a comprehensive evaluation of our method and various baselines for neural field and mesh deformation which show both pipelines achieve impressive efficiency and notable improvements in terms of quality of results and robustness. With our novel pipeline, we introduce a scalable approach to solve a well-established geometry processing problem on high-resolution meshes, and pave the way for extending other geometric tasks to the domain of implicit surfaces via local patch meshing.

Fluid Dynamics Network: Topology-Agnostic 4D Reconstruction via Fluid Dynamics Priors

Representing 3D surfaces as level sets of continuous functions over $\mathbb{R}^3$ is the common denominator of neural implicit representations, which recently enabled remarkable progress in geometric deep learning and computer vision tasks. In order to represent 3D motion within this framework, it is often assumed (either explicitly or implicitly) that the transformations which a surface may undergo are homeomorphic: this is not necessarily true, for instance, in the case of fluid dynamics. In order to represent more general classes of deformations, we propose to apply this theoretical framework as regularizers for the optimization of simple 4D implicit functions (such as signed distance fields). We show that our representation is capable of capturing both homeomorphic and topology-changing deformations, while also defining correspondences over the continuously-reconstructed surfaces.

Spectral Unions of Partial Deformable 3D Shapes

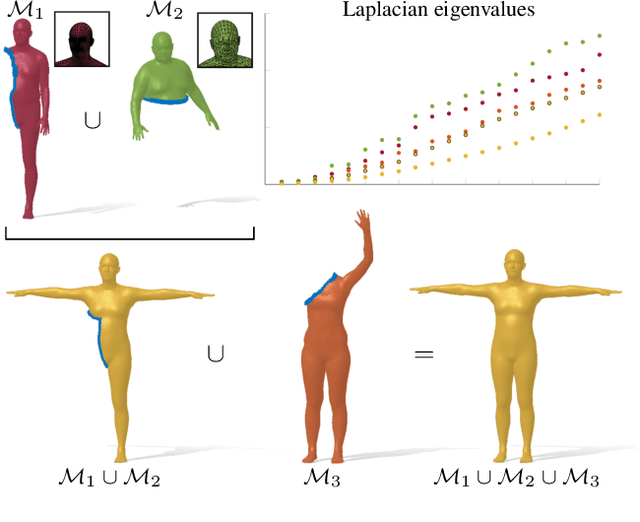
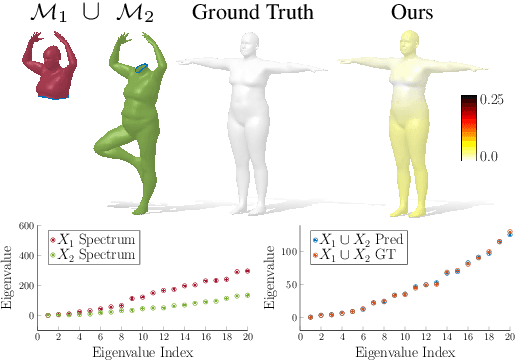
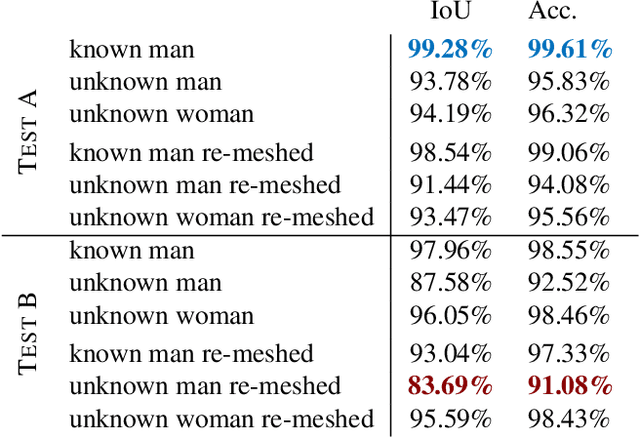
Spectral geometric methods have brought revolutionary changes to the field of geometry processing -- however, when the data to be processed exhibits severe partiality, such methods fail to generalize. As a result, there exists a big performance gap between methods dealing with complete shapes, and methods that address missing geometry. In this paper, we propose a possible way to fill this gap. We introduce the first method to compute compositions of non-rigidly deforming shapes, without requiring to solve first for a dense correspondence between the given partial shapes. We do so by operating in a purely spectral domain, where we define a union operation between short sequences of eigenvalues. Working with eigenvalues allows to deal with unknown correspondence, different sampling, and different discretization (point clouds and meshes alike), making this operation especially robust and general. Our approach is data-driven, and can generalize to isometric and non-isometric deformations of the surface, as long as these stay within the same semantic class (e.g., human bodies), as well as to partiality artifacts not seen at training time.