Fluid Dynamics Network: Topology-Agnostic 4D Reconstruction via Fluid Dynamics Priors

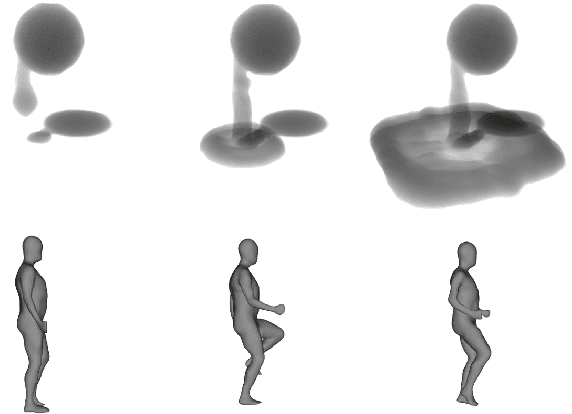
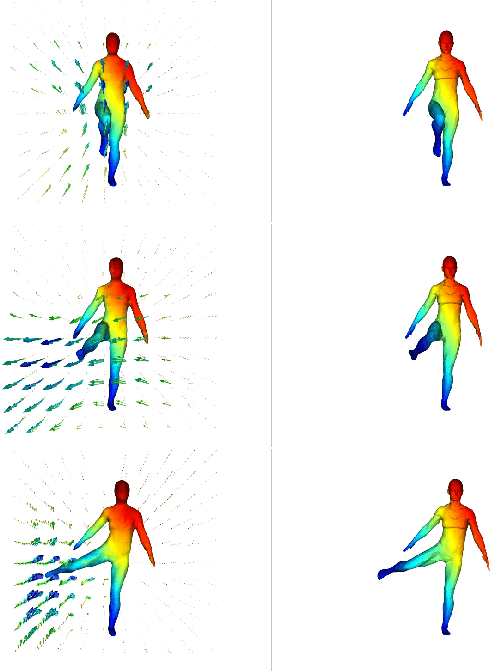
Representing 3D surfaces as level sets of continuous functions over $\mathbb{R}^3$ is the common denominator of neural implicit representations, which recently enabled remarkable progress in geometric deep learning and computer vision tasks. In order to represent 3D motion within this framework, it is often assumed (either explicitly or implicitly) that the transformations which a surface may undergo are homeomorphic: this is not necessarily true, for instance, in the case of fluid dynamics. In order to represent more general classes of deformations, we propose to apply this theoretical framework as regularizers for the optimization of simple 4D implicit functions (such as signed distance fields). We show that our representation is capable of capturing both homeomorphic and topology-changing deformations, while also defining correspondences over the continuously-reconstructed surfaces.