Verifying Properties of Tsetlin Machines

Tsetlin Machines (TsMs) are a promising and interpretable machine learning method which can be applied for various classification tasks. We present an exact encoding of TsMs into propositional logic and formally verify properties of TsMs using a SAT solver. In particular, we introduce in this work a notion of similarity of machine learning models and apply our notion to check for similarity of TsMs. We also consider notions of robustness and equivalence from the literature and adapt them for TsMs. Then, we show the correctness of our encoding and provide results for the properties: adversarial robustness, equivalence, and similarity of TsMs. In our experiments, we employ the MNIST and IMDB datasets for (respectively) image and sentiment classification. We discuss the results for verifying robustness obtained with TsMs with those in the literature obtained with Binarized Neural Networks on MNIST.

Extracting Rules from Neural Networks with Partial Interpretations

We investigate the problem of extracting rules, expressed in Horn logic, from neural network models. Our work is based on the exact learning model, in which a learner interacts with a teacher (the neural network model) via queries in order to learn an abstract target concept, which in our case is a set of Horn rules. We consider partial interpretations to formulate the queries. These can be understood as a representation of the world where part of the knowledge regarding the truthiness of propositions is unknown. We employ Angluin s algorithm for learning Horn rules via queries and evaluate our strategy empirically.

On the Learnability of Possibilistic Theories

We investigate learnability of possibilistic theories from entailments in light of Angluin's exact learning model. We consider cases in which only membership, only equivalence, and both kinds of queries can be posed by the learner. We then show that, for a large class of problems, polynomial time learnability results for classical logic can be transferred to the respective possibilistic extension. In particular, it follows from our results that the possibilistic extension of propositional Horn theories is exactly learnable in polynomial time. As polynomial time learnability in the exact model is transferable to the classical probably approximately correct model extended with membership queries, our work also establishes such results in this model.

Learning Query Inseparable ELH Ontologies

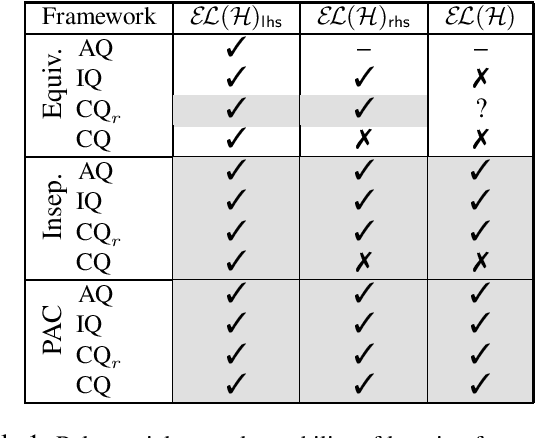
We investigate the complexity of learning query inseparable ELH ontologies in a variant of Angluin's exact learning model. Given a fixed data instance A* and a query language Q, we are interested in computing an ontology H that entails the same queries as a target ontology T on A*, that is, H and T are inseparable w.r.t. A* and Q. The learner is allowed to pose two kinds of questions. The first is `Does (T,A)\models q?', with A an arbitrary data instance and q and query in Q. An oracle replies this question with `yes' or `no'. In the second, the learner asks `Are H and T inseparable w.r.t. A* and Q?'. If so, the learning process finishes, otherwise, the learner receives (A*,q) with q in Q, (T,A*)\models q and (H,A*)\not\models q (or vice-versa). Then, we analyse conditions in which query inseparability is preserved if A* changes. Finally, we consider the PAC learning model and a setting where the algorithms learn from a batch of classified data, limiting interactions with the oracles.