Dynamic Epistemic Logic Games with Epistemic Temporal Goals

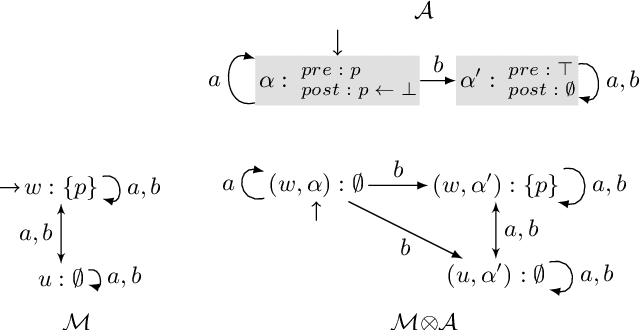
Dynamic Epistemic Logic (DEL) is a logical framework in which one can describe in great detail how actions are perceived by the agents, and how they affect the world. DEL games were recently introduced as a way to define classes of games with imperfect information where the actions available to the players are described very precisely. This framework makes it possible to define easily, for instance, classes of games where players can only use public actions or public announcements. These games have been studied for reachability objectives, where the aim is to reach a situation satisfying some epistemic property expressed in epistemic logic; several (un)decidability results have been established. In this work we show that the decidability results obtained for reachability objectives extend to a much more general class of winning conditions, namely those expressible in the epistemic temporal logic LTLK. To do so we establish that the infinite game structures generated by DEL public actions are regular, and we describe how to obtain finite representations on which we rely to solve them.

Refinement Modal Logic

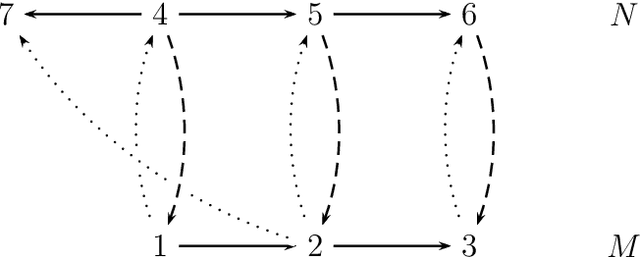
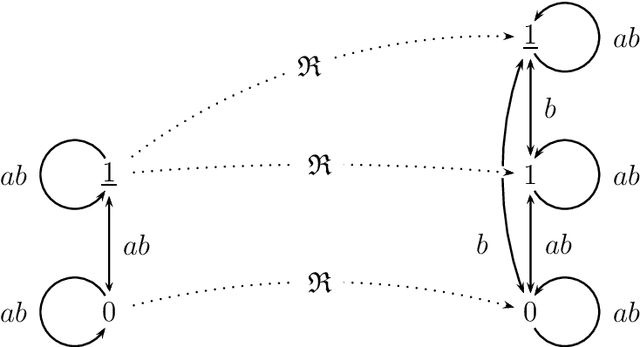
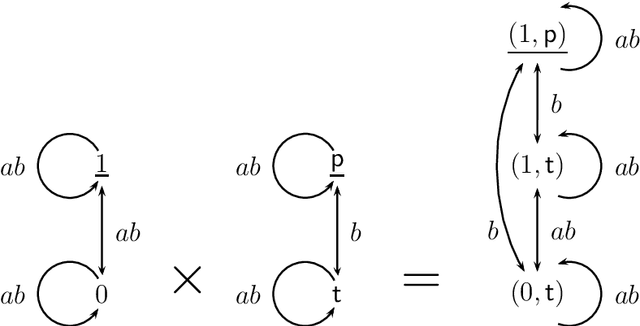
In this paper we present {\em refinement modal logic}. A refinement is like a bisimulation, except that from the three relational requirements only `atoms' and `back' need to be satisfied. Our logic contains a new operator 'all' in addition to the standard modalities 'box' for each agent. The operator 'all' acts as a quantifier over the set of all refinements of a given model. As a variation on a bisimulation quantifier, this refinement operator or refinement quantifier 'all' can be seen as quantifying over a variable not occurring in the formula bound by it. The logic combines the simplicity of multi-agent modal logic with some powers of monadic second-order quantification. We present a sound and complete axiomatization of multi-agent refinement modal logic. We also present an extension of the logic to the modal mu-calculus, and an axiomatization for the single-agent version of this logic. Examples and applications are also discussed: to software verification and design (the set of agents can also be seen as a set of actions), and to dynamic epistemic logic. We further give detailed results on the complexity of satisfiability, and on succinctness.