A Data-Driven Framework for Identifying Investment Opportunities in Private Equity

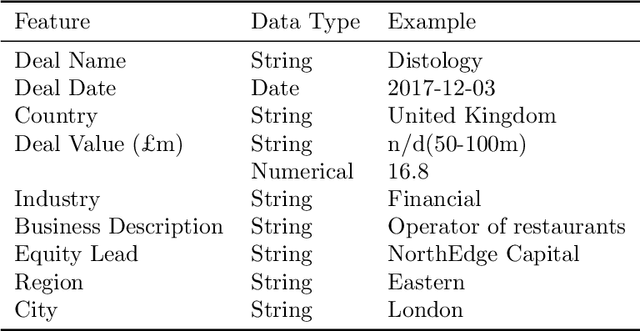
The core activity of a Private Equity (PE) firm is to invest into companies in order to provide the investors with profit, usually within 4-7 years. To invest into a company or not is typically done manually by looking at various performance indicators of the company and then making a decision often based on instinct. This process is rather unmanageable given the large number of companies to potentially invest. Moreover, as more data about company performance indicators becomes available and the number of different indicators one may want to consider increases, manual crawling and assessment of investment opportunities becomes inefficient and ultimately impossible. To address these issues, this paper proposes a framework for automated data-driven screening of investment opportunities and thus the recommendation of businesses to invest in. The framework draws on data from several sources to assess the financial and managerial position of a company, and then uses an explainable artificial intelligence (XAI) engine to suggest investment recommendations. The robustness of the model is validated using different AI algorithms, class imbalance-handling methods, and features extracted from the available data sources.

Refinement Modal Logic

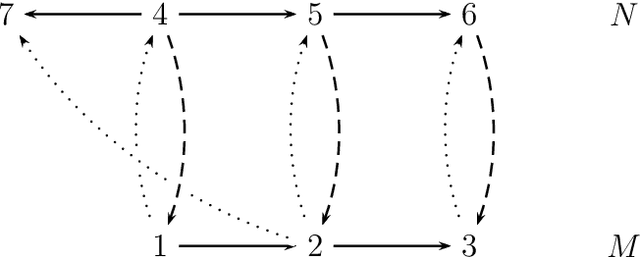
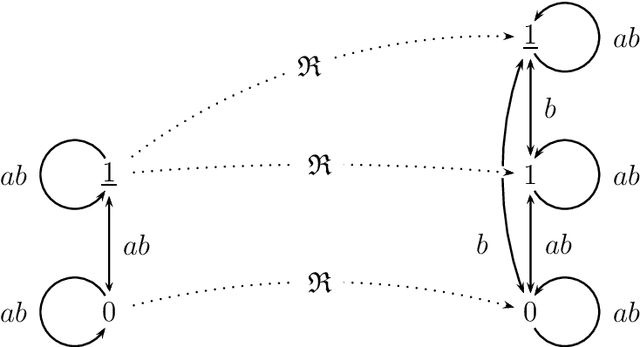
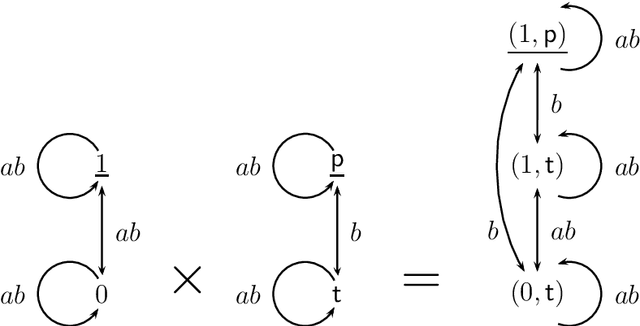
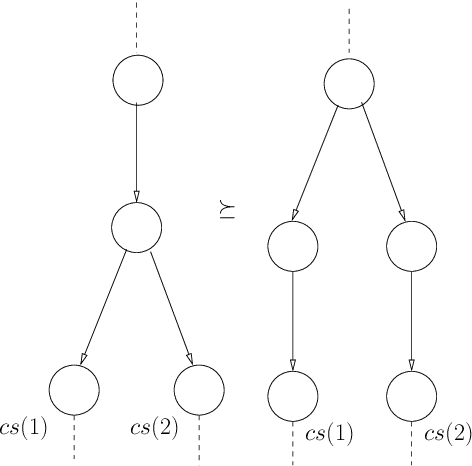
In this paper we present {\em refinement modal logic}. A refinement is like a bisimulation, except that from the three relational requirements only `atoms' and `back' need to be satisfied. Our logic contains a new operator 'all' in addition to the standard modalities 'box' for each agent. The operator 'all' acts as a quantifier over the set of all refinements of a given model. As a variation on a bisimulation quantifier, this refinement operator or refinement quantifier 'all' can be seen as quantifying over a variable not occurring in the formula bound by it. The logic combines the simplicity of multi-agent modal logic with some powers of monadic second-order quantification. We present a sound and complete axiomatization of multi-agent refinement modal logic. We also present an extension of the logic to the modal mu-calculus, and an axiomatization for the single-agent version of this logic. Examples and applications are also discussed: to software verification and design (the set of agents can also be seen as a set of actions), and to dynamic epistemic logic. We further give detailed results on the complexity of satisfiability, and on succinctness.