Causal Reinforcement Learning for Complex Card Games: A Magic The Gathering Benchmark

Causal reinforcement learning (RL) lacks benchmarks for complex systems that combine sequential decision making, hidden information, large masked action spaces, and explicit causal structure. We introduce MTG-Causal-RL, a Gymnasium benchmark built on Magic: The Gathering with a 3,077-dimensional partial observation, a 478-action masked discrete action space, five competitive Standard archetypes, three reward schemes, and a hand-specified Structural Causal Model (SCM) over strategic variables. Every episode exposes causal variables, SCM-predicted intervention effects, and per-factor credit traces, making causal credit assignment, leave-one-out cross-archetype transfer, and policy auditability first-class metrics. We adapt a panel of reference baselines: random, heuristic, masked PPO, a causal-world-model PPO variant, and an architecture-matched scalar control. We propose Causal Graph-Factored Advantage PPO (CGFA-PPO) as a reference causal agent that uses SCM parents of win probability as factor-aligned critic targets with an intervention-calibration loss. All comparisons use paired seeds, paired-bootstrap confidence intervals, and Holm-Bonferroni correction within pre-registered families. Masked PPO and CGFA-PPO reach competitive in-distribution win rates and exceed the random baseline; per-factor calibration trajectories and leave-one-out transfer gaps expose diagnostic structure that scalar win rate alone cannot. We release the benchmark, reference-baseline results, and full evaluation protocol openly. By coupling a strategically rich, partially observed domain with an explicit causal interface and statistical protocol, MTG-Causal-RL gives causal-RL, world-model, and LLM-agent research a shared testbed for questions current benchmarks cannot pose together: causal credit assignment under masked action spaces, structural transfer across archetypes, and SCM-grounded policy auditability.

PODiff: Latent Diffusion in Proper Orthogonal Decomposition Space for Scientific Super-Resolution

Probabilistic super-resolution of high-dimensional spatial fields using diffusion models is often computationally prohibitive due to the cost of operating directly in pixel space. We propose PODiff, a structured conditional generative framework that performs diffusion in a fixed, variance-ordered Proper Orthogonal Decomposition (POD) coefficient space, exploiting the orthogonality of POD modes to impose an interpretable, variance-ordered latent geometry. This design enables efficient ensemble generation, preserves dominant spatial structure, and yields spatially interpretable, well-calibrated uncertainty at substantially lower computational cost. We evaluate PODiff on sea surface temperature downscaling over the West Australian coast and on a controlled advection-diffusion benchmark. PODiff achieves reconstruction accuracy comparable to pixel-space diffusion while requiring significantly less memory and producing more reliable uncertainty estimates than deterministic and Monte Carlo Dropout baselines.

Unifying Causal Reinforcement Learning: Survey, Taxonomy, Algorithms and Applications

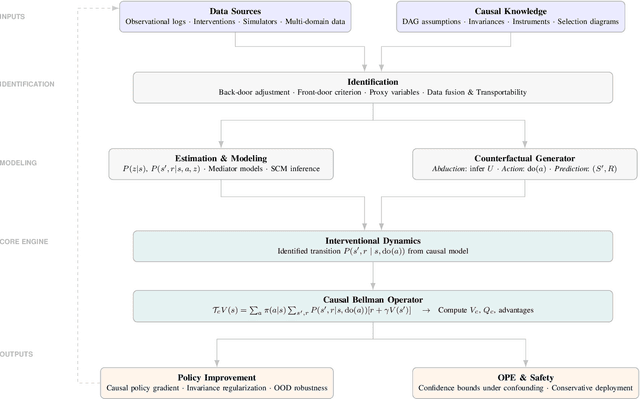
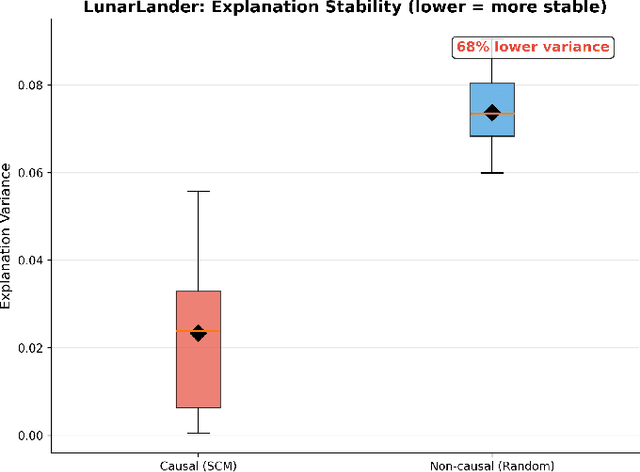
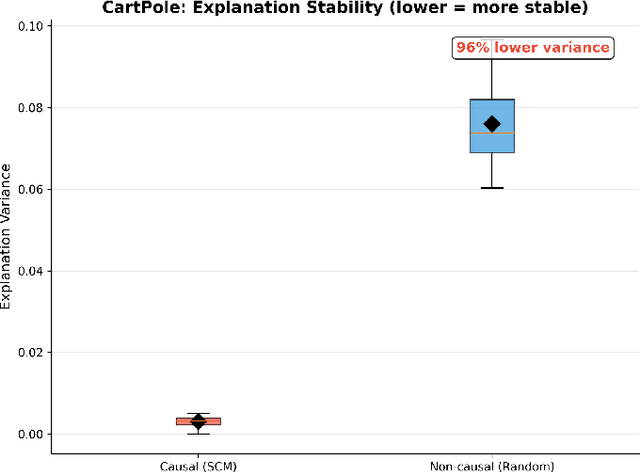
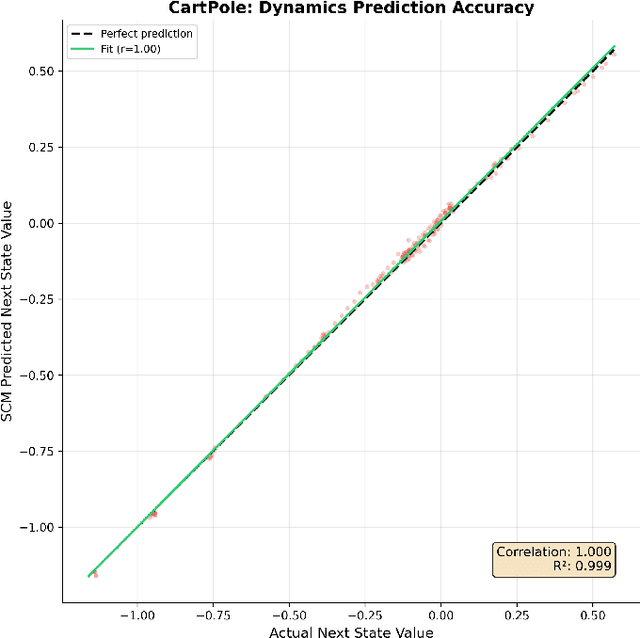
Integrating causal inference (CI) with reinforcement learning (RL) has emerged as a powerful paradigm to address critical limitations in classical RL, including low explainability, lack of robustness and generalization failures. Traditional RL techniques, which typically rely on correlation-driven decision-making, struggle when faced with distribution shifts, confounding variables, and dynamic environments. Causal reinforcement learning (CRL), leveraging the foundational principles of causal inference, offers promising solutions to these challenges by explicitly modeling cause-and-effect relationships. In this survey, we systematically review recent advancements at the intersection of causal inference and RL. We categorize existing approaches into causal representation learning, counterfactual policy optimization, offline causal RL, causal transfer learning, and causal explainability. Through this structured analysis, we identify prevailing challenges, highlight empirical successes in practical applications, and discuss open problems. Finally, we provide future research directions, underscoring the potential of CRL for developing robust, generalizable, and interpretable artificial intelligence systems.

NatADiff: Adversarial Boundary Guidance for Natural Adversarial Diffusion

Adversarial samples exploit irregularities in the manifold ``learned'' by deep learning models to cause misclassifications. The study of these adversarial samples provides insight into the features a model uses to classify inputs, which can be leveraged to improve robustness against future attacks. However, much of the existing literature focuses on constrained adversarial samples, which do not accurately reflect test-time errors encountered in real-world settings. To address this, we propose `NatADiff', an adversarial sampling scheme that leverages denoising diffusion to generate natural adversarial samples. Our approach is based on the observation that natural adversarial samples frequently contain structural elements from the adversarial class. Deep learning models can exploit these structural elements to shortcut the classification process, rather than learning to genuinely distinguish between classes. To leverage this behavior, we guide the diffusion trajectory towards the intersection of the true and adversarial classes, combining time-travel sampling with augmented classifier guidance to enhance attack transferability while preserving image fidelity. Our method achieves comparable attack success rates to current state-of-the-art techniques, while exhibiting significantly higher transferability across model architectures and better alignment with natural test-time errors as measured by FID. These results demonstrate that NatADiff produces adversarial samples that not only transfer more effectively across models, but more faithfully resemble naturally occurring test-time errors.

Q-Cogni: An Integrated Causal Reinforcement Learning Framework

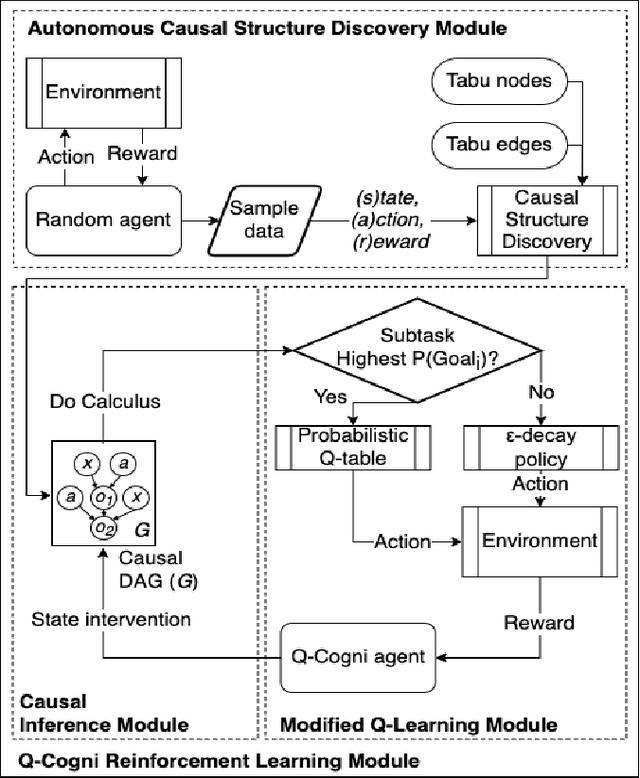
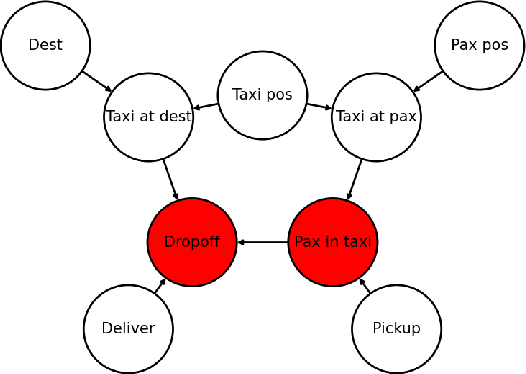
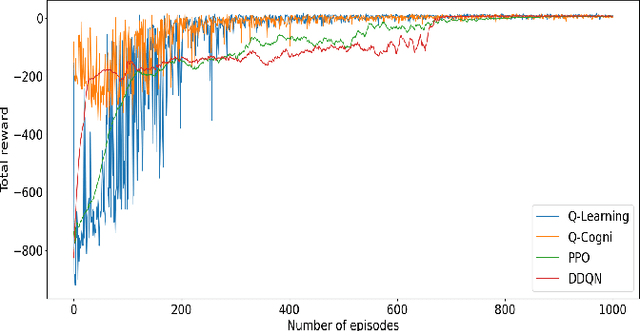
We present Q-Cogni, an algorithmically integrated causal reinforcement learning framework that redesigns Q-Learning with an autonomous causal structure discovery method to improve the learning process with causal inference. Q-Cogni achieves optimal learning with a pre-learned structural causal model of the environment that can be queried during the learning process to infer cause-and-effect relationships embedded in a state-action space. We leverage on the sample efficient techniques of reinforcement learning, enable reasoning about a broader set of policies and bring higher degrees of interpretability to decisions made by the reinforcement learning agent. We apply Q-Cogni on the Vehicle Routing Problem (VRP) and compare against state-of-the-art reinforcement learning algorithms. We report results that demonstrate better policies, improved learning efficiency and superior interpretability of the agent's decision making. We also compare this approach with traditional shortest-path search algorithms and demonstrate the benefits of our causal reinforcement learning framework to high dimensional problems. Finally, we apply Q-Cogni to derive optimal routing decisions for taxis in New York City using the Taxi & Limousine Commission trip record data and compare with shortest-path search, reporting results that show 85% of the cases with an equal or better policy derived from Q-Cogni in a real-world domain.

Aleatoric Description Logic for Probailistic Reasoning (Long Version)

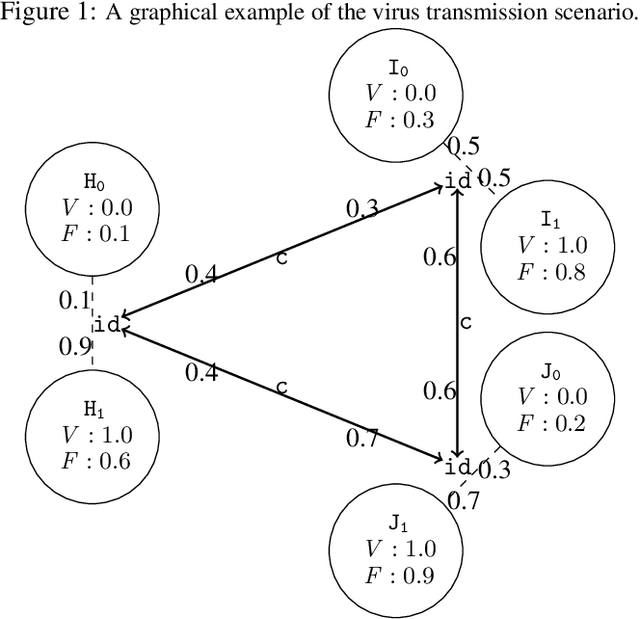
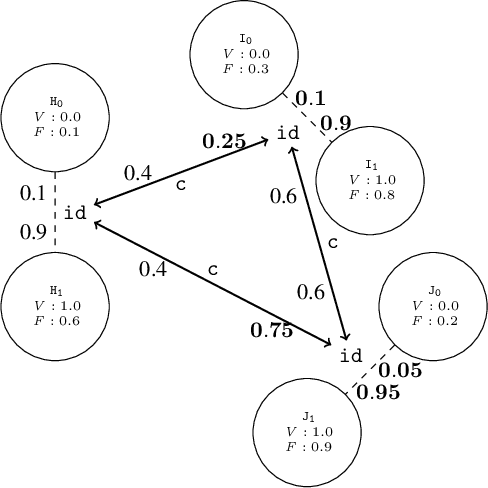
Description logics are a powerful tool for describing ontological knowledge bases. That is, they give a factual account of the world in terms of individuals, concepts and relations. In the presence of uncertainty, such factual accounts are not feasible, and a subjective or epistemic approach is required. Aleatoric description logic models uncertainty in the world as aleatoric events, by the roll of the dice, where an agent has subjective beliefs about the bias of these dice. This provides a subjective Bayesian description logic, where propositions and relations are assigned probabilities according to what a rational agent would bet, given a configuration of possible individuals and dice. Aleatoric description logic is shown to generalise the description logic ALC, and can be seen to describe a probability space of interpretations of a restriction of ALC where all roles are functions. Several computational problems are considered and model-checking and consistency checking algorithms are presented. Finally, aleatoric description logic is shown to be able to model learning, where agents are able to condition their beliefs on the bias of dice according to observations.

Refinement Modal Logic

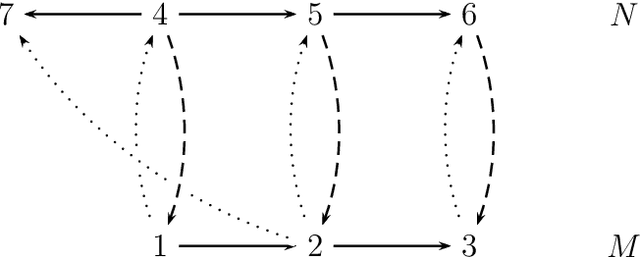
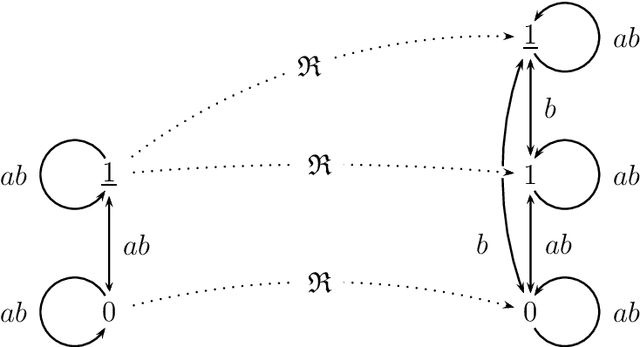
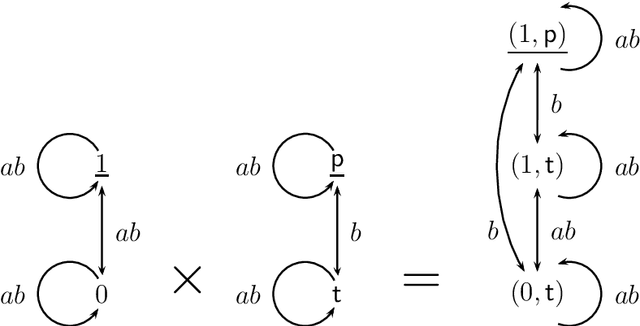
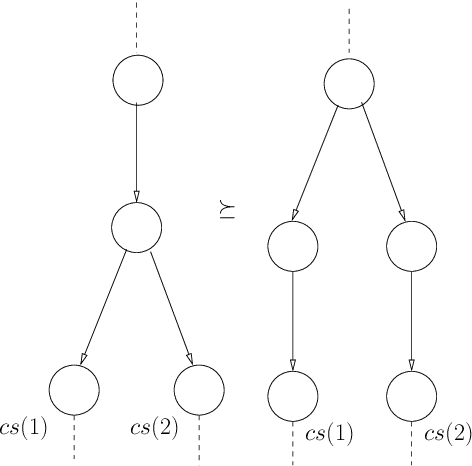
In this paper we present {\em refinement modal logic}. A refinement is like a bisimulation, except that from the three relational requirements only `atoms' and `back' need to be satisfied. Our logic contains a new operator 'all' in addition to the standard modalities 'box' for each agent. The operator 'all' acts as a quantifier over the set of all refinements of a given model. As a variation on a bisimulation quantifier, this refinement operator or refinement quantifier 'all' can be seen as quantifying over a variable not occurring in the formula bound by it. The logic combines the simplicity of multi-agent modal logic with some powers of monadic second-order quantification. We present a sound and complete axiomatization of multi-agent refinement modal logic. We also present an extension of the logic to the modal mu-calculus, and an axiomatization for the single-agent version of this logic. Examples and applications are also discussed: to software verification and design (the set of agents can also be seen as a set of actions), and to dynamic epistemic logic. We further give detailed results on the complexity of satisfiability, and on succinctness.