Tom Smoker
Aleatoric Description Logic for Probailistic Reasoning (Long Version)
Aug 30, 2021
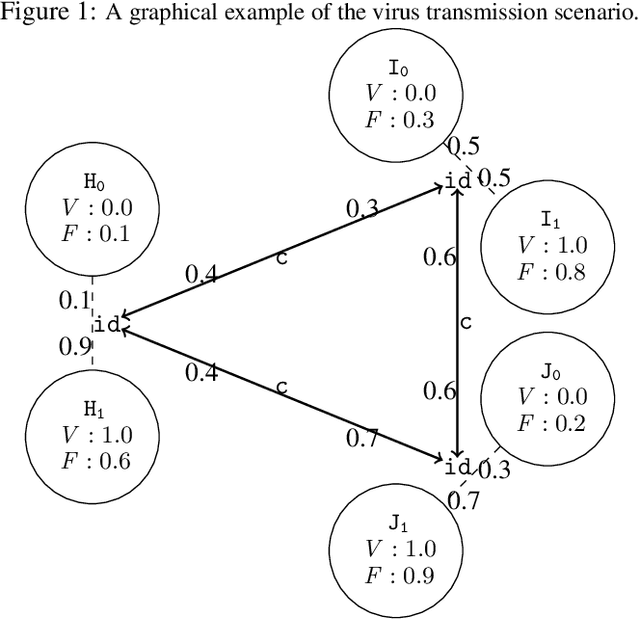
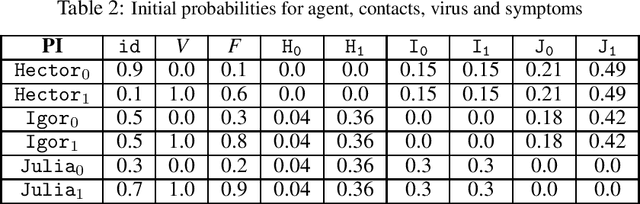
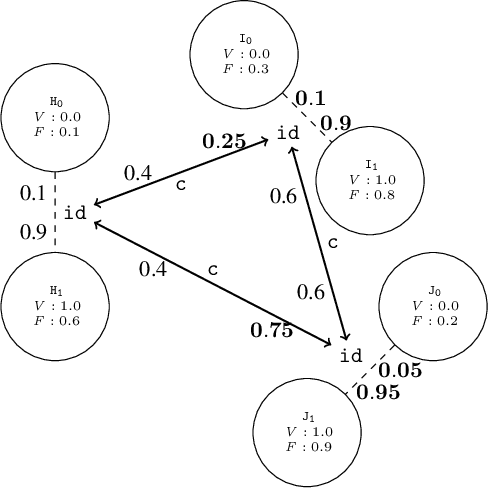
Abstract:Description logics are a powerful tool for describing ontological knowledge bases. That is, they give a factual account of the world in terms of individuals, concepts and relations. In the presence of uncertainty, such factual accounts are not feasible, and a subjective or epistemic approach is required. Aleatoric description logic models uncertainty in the world as aleatoric events, by the roll of the dice, where an agent has subjective beliefs about the bias of these dice. This provides a subjective Bayesian description logic, where propositions and relations are assigned probabilities according to what a rational agent would bet, given a configuration of possible individuals and dice. Aleatoric description logic is shown to generalise the description logic ALC, and can be seen to describe a probability space of interpretations of a restriction of ALC where all roles are functions. Several computational problems are considered and model-checking and consistency checking algorithms are presented. Finally, aleatoric description logic is shown to be able to model learning, where agents are able to condition their beliefs on the bias of dice according to observations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge