Defeasible reasoning in Description Logics: an overview on DL^N

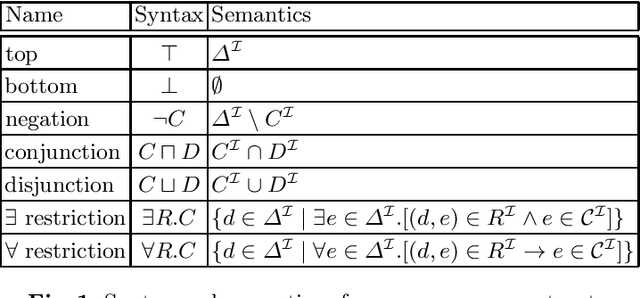
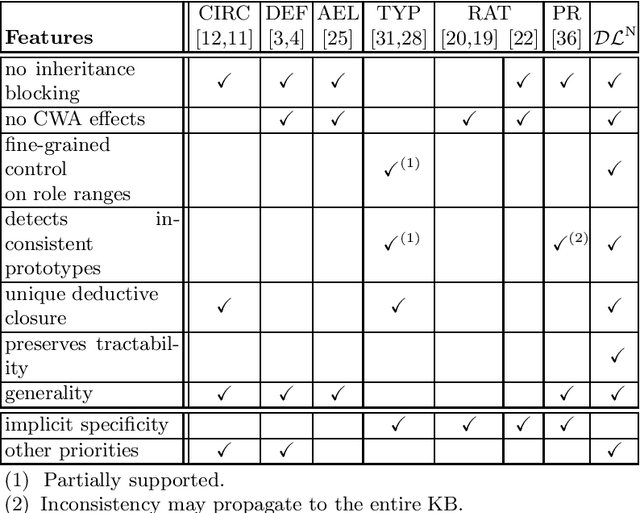
DL^N is a recent approach that extends description logics with defeasible reasoning capabilities. In this paper we provide an overview on DL^N, illustrating the underlying knowledge engineering requirements as well as the characteristic features that preserve DL^N from some recurrent semantic and computational drawbacks. We also compare DL^N with some alternative nonmonotonic semantics, enlightening the relationships between the KLM postulates and DL^N.

Machine Understandable Policies and GDPR Compliance Checking

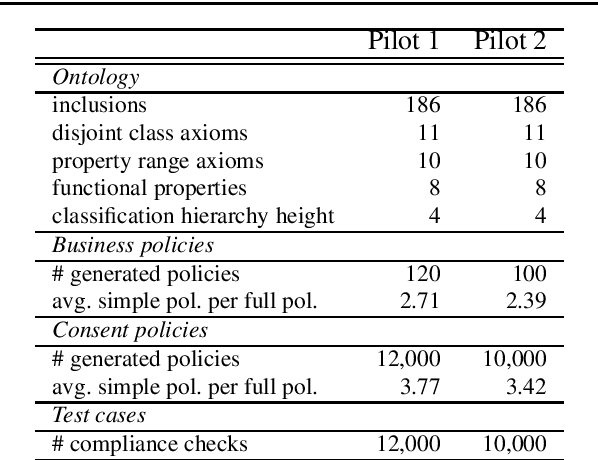
The European General Data Protection Regulation (GDPR) calls for technical and organizational measures to support its implementation. Towards this end, the SPECIAL H2020 project aims to provide a set of tools that can be used by data controllers and processors to automatically check if personal data processing and sharing complies with the obligations set forth in the GDPR. The primary contributions of the project include: (i) a policy language that can be used to express consent, business policies, and regulatory obligations; and (ii) two different approaches to automated compliance checking that can be used to demonstrate that data processing performed by data controllers / processors complies with consent provided by data subjects, and business processes comply with regulatory obligations set forth in the GDPR.

Defeasible Inclusions in Low-Complexity DLs

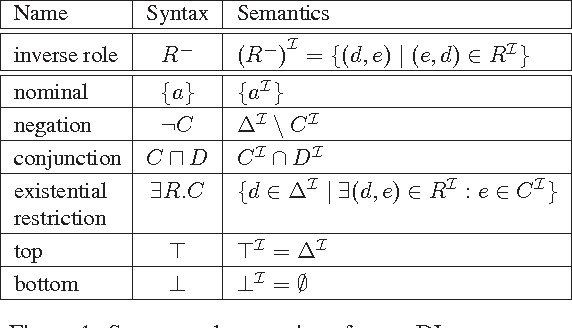
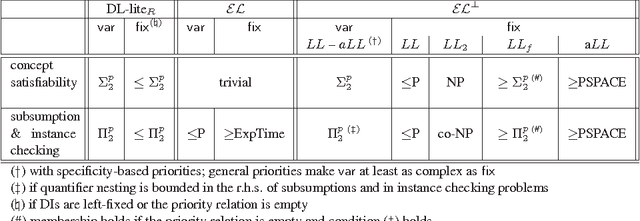
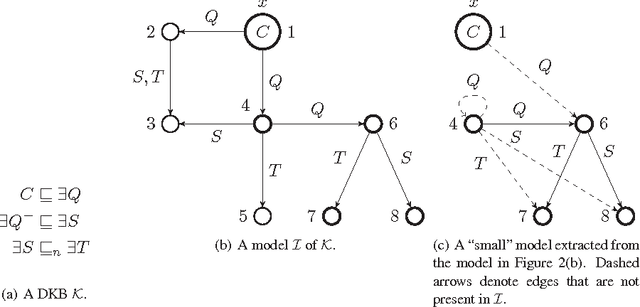
Some of the applications of OWL and RDF (e.g. biomedical knowledge representation and semantic policy formulation) call for extensions of these languages with nonmonotonic constructs such as inheritance with overriding. Nonmonotonic description logics have been studied for many years, however no practical such knowledge representation languages exist, due to a combination of semantic difficulties and high computational complexity. Independently, low-complexity description logics such as DL-lite and EL have been introduced and incorporated in the OWL standard. Therefore, it is interesting to see whether the syntactic restrictions characterizing DL-lite and EL bring computational benefits to their nonmonotonic versions, too. In this paper we extensively investigate the computational complexity of Circumscription when knowledge bases are formulated in DL-lite_R, EL, and fragments thereof. We identify fragments whose complexity ranges from P to the second level of the polynomial hierarchy, as well as fragments whose complexity raises to PSPACE and beyond.

The Complexity of Circumscription in DLs

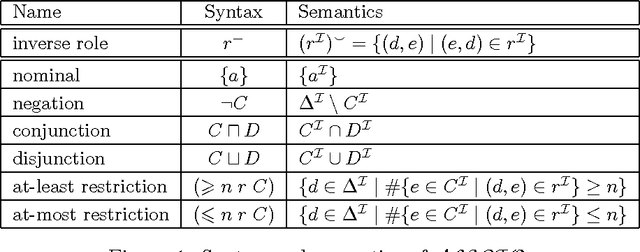
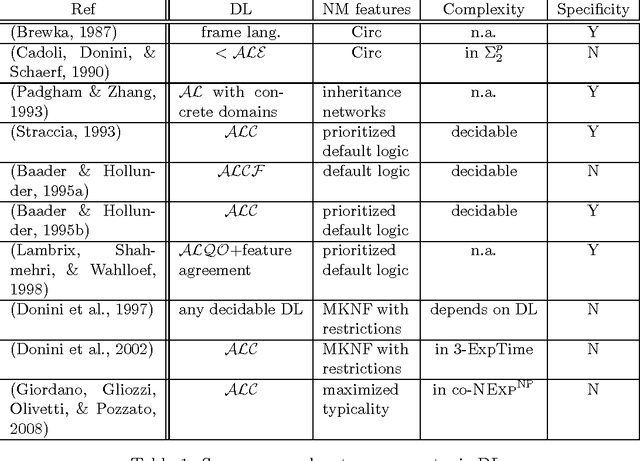
As fragments of first-order logic, Description logics (DLs) do not provide nonmonotonic features such as defeasible inheritance and default rules. Since many applications would benefit from the availability of such features, several families of nonmonotonic DLs have been developed that are mostly based on default logic and autoepistemic logic. In this paper, we consider circumscription as an interesting alternative approach to nonmonotonic DLs that, in particular, supports defeasible inheritance in a natural way. We study DLs extended with circumscription under different language restrictions and under different constraints on the sets of minimized, fixed, and varying predicates, and pinpoint the exact computational complexity of reasoning for DLs ranging from ALC to ALCIO and ALCQO. When the minimized and fixed predicates include only concept names but no role names, then reasoning is complete for NExpTime^NP. It becomes complete for NP^NExpTime when the number of minimized and fixed predicates is bounded by a constant. If roles can be minimized or fixed, then complexity ranges from NExpTime^NP to undecidability.

A decidable subclass of finitary programs

Answer set programming - the most popular problem solving paradigm based on logic programs - has been recently extended to support uninterpreted function symbols. All of these approaches have some limitation. In this paper we propose a class of programs called FP2 that enjoys a different trade-off between expressiveness and complexity. FP2 programs enjoy the following unique combination of properties: (i) the ability of expressing predicates with infinite extensions; (ii) full support for predicates with arbitrary arity; (iii) decidability of FP2 membership checking; (iv) decidability of skeptical and credulous stable model reasoning for call-safe queries. Odd cycles are supported by composing FP2 programs with argument restricted programs.

On finitely recursive programs

Disjunctive finitary programs are a class of logic programs admitting function symbols and hence infinite domains. They have very good computational properties, for example ground queries are decidable while in the general case the stable model semantics is highly undecidable. In this paper we prove that a larger class of programs, called finitely recursive programs, preserves most of the good properties of finitary programs under the stable model semantics, namely: (i) finitely recursive programs enjoy a compactness property; (ii) inconsistency checking and skeptical reasoning are semidecidable; (iii) skeptical resolution is complete for normal finitely recursive programs. Moreover, we show how to check inconsistency and answer skeptical queries using finite subsets of the ground program instantiation. We achieve this by extending the splitting sequence theorem by Lifschitz and Turner: We prove that if the input program P is finitely recursive, then the partial stable models determined by any smooth splitting omega-sequence converge to a stable model of P.

The Complexity of Enriched Mu-Calculi

The fully enriched μ-calculus is the extension of the propositional μ-calculus with inverse programs, graded modalities, and nominals. While satisfiability in several expressive fragments of the fully enriched μ-calculus is known to be decidable and ExpTime-complete, it has recently been proved that the full calculus is undecidable. In this paper, we study the fragments of the fully enriched μ-calculus that are obtained by dropping at least one of the additional constructs. We show that, in all fragments obtained in this way, satisfiability is decidable and ExpTime-complete. Thus, we identify a family of decidable logics that are maximal (and incomparable) in expressive power. Our results are obtained by introducing two new automata models, showing that their emptiness problems are ExpTime-complete, and then reducing satisfiability in the relevant logics to these problems. The automata models we introduce are two-way graded alternating parity automata over infinite trees (2GAPTs) and fully enriched automata (FEAs) over infinite forests. The former are a common generalization of two incomparable automata models from the literature. The latter extend alternating automata in a similar way as the fully enriched μ-calculus extends the standard μ-calculus.

Abduction, ASP and Open Logic Programs

Open logic programs and open entailment have been recently proposed as an abstract framework for the verification of incomplete specifications based upon normal logic programs and the stable model semantics. There are obvious analogies between open predicates and abducible predicates. However, despite superficial similarities, there are features of open programs that have no immediate counterpart in the framework of abduction and viceversa. Similarly, open programs cannot be immediately simulated with answer set programming (ASP). In this paper we start a thorough investigation of the relationships between open inference, abduction and ASP. We shall prove that open programs generalize the other two frameworks. The generalized framework suggests interesting extensions of abduction under the generalized stable model semantics. In some cases, we will be able to reduce open inference to abduction and ASP, thereby estimating its computational complexity. At the same time, the aforementioned reduction opens the way to new applications of abduction and ASP.