Aurélie Beynier
Perspectives for Direct Interpretability in Multi-Agent Deep Reinforcement Learning
Feb 02, 2025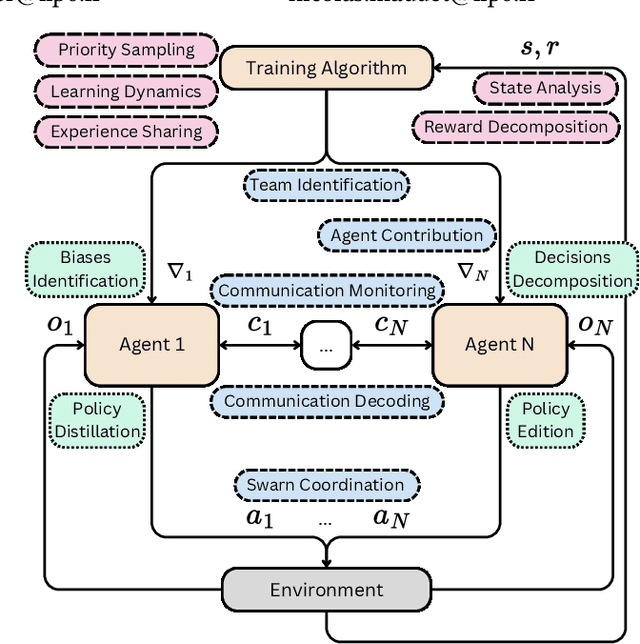
Abstract:Multi-Agent Deep Reinforcement Learning (MADRL) was proven efficient in solving complex problems in robotics or games, yet most of the trained models are hard to interpret. While learning intrinsically interpretable models remains a prominent approach, its scalability and flexibility are limited in handling complex tasks or multi-agent dynamics. This paper advocates for direct interpretability, generating post hoc explanations directly from trained models, as a versatile and scalable alternative, offering insights into agents' behaviour, emergent phenomena, and biases without altering models' architectures. We explore modern methods, including relevance backpropagation, knowledge edition, model steering, activation patching, sparse autoencoders and circuit discovery, to highlight their applicability to single-agent, multi-agent, and training process challenges. By addressing MADRL interpretability, we propose directions aiming to advance active topics such as team identification, swarm coordination and sample efficiency.
An Optimal Procedure to Check Pareto-Optimality in House Markets with Single-Peaked Preferences
Feb 14, 2020
Abstract:Recently, the problem of allocating one resource per agent with initial endowments (house markets) has seen a renewed interest: indeed, while in the domain of strict preferences the Top Trading Cycle algorithm is known to be the only procedure guaranteeing Pareto-optimality, individual rationality, and strategy proofness. However, the situation differs in the single-peaked domain. Indeed, Bade presented the Crawler, an alternative procedure enjoying the same properties, with the additional advantage of being implementable in obviously dominant strategies. In this paper we further investigate the Crawler and propose the Diver, a variant which checks optimally whether an allocation is Pareto-optimal for single-peaked preferences, thus improving over known techniques used for checking Pareto-optimality in more general domains. We also prove that the Diver is asymptotically optimal in terms of communication complexity.
Fair in the Eyes of Others
Nov 25, 2019

Abstract:Envy-freeness is a widely studied notion in resource allocation, capturing some aspects of fairness. The notion of envy being inherently subjective though, it might be the case that an agent envies another agent, but that she objectively has no reason to do so. The difficulty here is to define the notion of objectivity, since no ground-truth can properly serve as a basis of this definition. A natural approach is to consider the judgement of the other agents as a proxy for objectivity. Building on previous work by Parijs (who introduced "unanimous envy") we propose the notion of approval envy: an agent $a_i$ experiences approval envy towards $a_j$ if she is envious of $a_j$, and sufficiently many agents agree that this should be the case, from their own perspectives. Some interesting properties of this notion are put forward. Computing the minimal threshold guaranteeing approval envy clearly inherits well-known intractable results from envy-freeness, but (i) we identify some tractable cases such as house allocation; and (ii) we provide a general method based on a mixed integer programming encoding of the problem, which proves to be efficient in practice. This allows us in particular to show experimentally that existence of such allocations, with a rather small threshold, is very often observed.
House Markets and Single-Peaked Preferences: From Centralized to Decentralized Allocation Procedures
Jun 24, 2019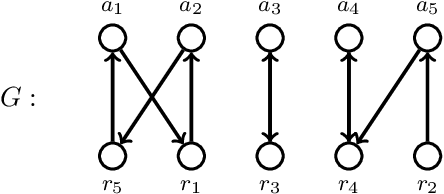
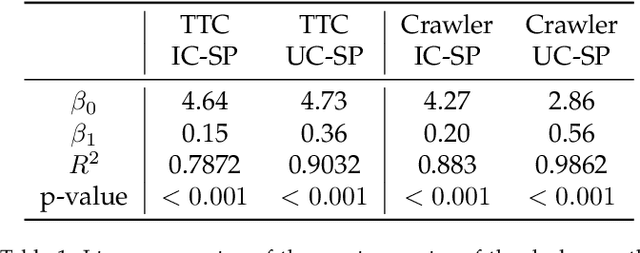
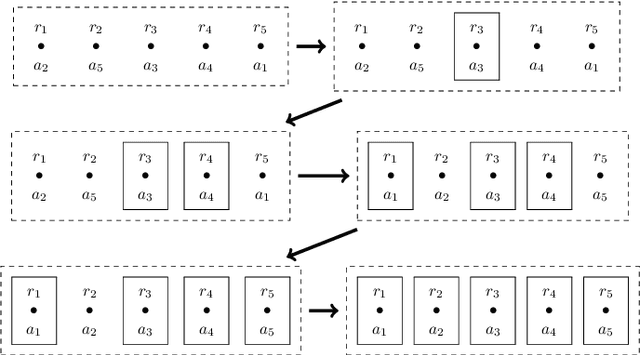
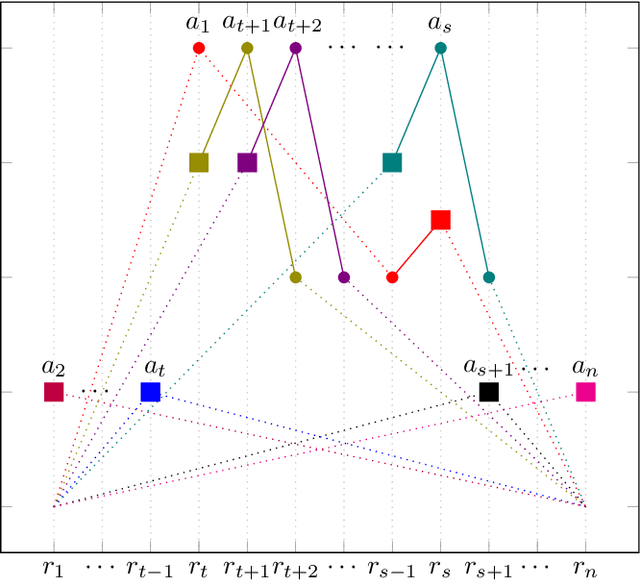
Abstract:Recently, the problem of allocating one resource per agent with initial endowments (\emph{house markets}) has seen a renewed interest: indeed, while in the general domain Top Trading Cycle is known to be the only procedure guaranteeing Pareto-optimality, individual rationality, and strategy proofness, the situation differs in single-peaked domains. Bade (2019) presented the Crawler, an alternative procedure enjoying the same properties (with the additional advantage of being implementable in obviously dominant strategies); while Damamme et al. (2015) showed that allowing mutually beneficial swap-deals among the agents was already enough to guarantee Pareto-optimality. In this paper we significantly deepen our understanding of this decentralized procedures: we show in particular that the single-peaked domains happen to be ``maximal'' if one wishes to guarantee this convergence property. Interestingly, we also observe that the set of allocations reachable by swap-deals always contains the outcome of the Crawler. To further investigate how these different mechanisms compare, we pay special attention to the average and minimum rank of the resource obtained by the agents in the outcome allocation. We provide theoretical bounds on the loss potentially induced by these procedures with respect to these criteria, and complement these results with an extensive experimental study which shows how different variants of swap dynamics behave. In fact, even the simplest dynamics exhibit very good results, and it is possible to further guide the process towards our objectives, if one is ready to sacrifice a bit in terms of decentralization. On our way, we also show that a simple variant of the Crawler allows to check efficiently that an allocation is Pareto-optimal in single-peaked domains.
Efficiency, Sequenceability and Deal-Optimality in Fair Division of Indivisible Goods
Jul 28, 2018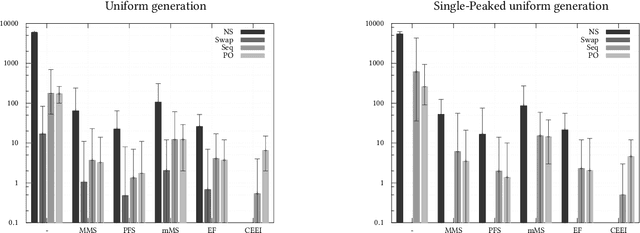
Abstract:In fair division of indivisible goods, using sequences of sincere choices (or picking sequences) is a natural way to allocate the objects. The idea is as follows: at each stage, a designated agent picks one object among those that remain. Another intuitive way to obtain an allocation is to give objects to agents in the first place, and to let agents exchange them as long as such "deals" are beneficial. This paper investigates these notions, when agents have additive preferences over objects, and unveils surprising connections between them, and with other efficiency and fairness notions. In particular, we show that an allocation is sequenceable iff it is optimal for a certain type of deals, namely cycle deals involving a single object. Furthermore, any Pareto-optimal allocation is sequenceable, but not the converse. Regarding fairness, we show that an allocation can be envy-free and non-sequenceable, but that every competitive equilibrium with equal incomes is sequenceable. To complete the picture, we show how some domain restrictions may affect the relations between these notions. Finally, we experimentally explore the links between the scales of efficiency and fairness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge